freshcoast
- 185
- 1
1. Problem statement
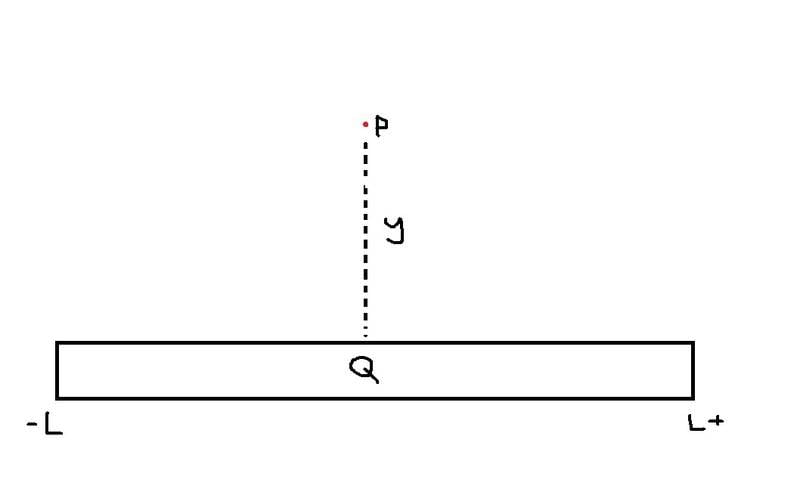
A thin rod of length 2L has charge Q uniformly distributed along its length.
1. Draw a graph of the charge density as a function of x from -L to L
2. Find the electric potential at point P a distance y away
3. Use the result in part 2 of the electric field at point P (you are finding the electric field as a function of a y equation)
4. Assess ; Draw the V versus y graph and draw the E versus y graph.
2. Known equations
v = k ∫ dq / r
e = -∇v
λ = Q / L
3. Attempt
1.
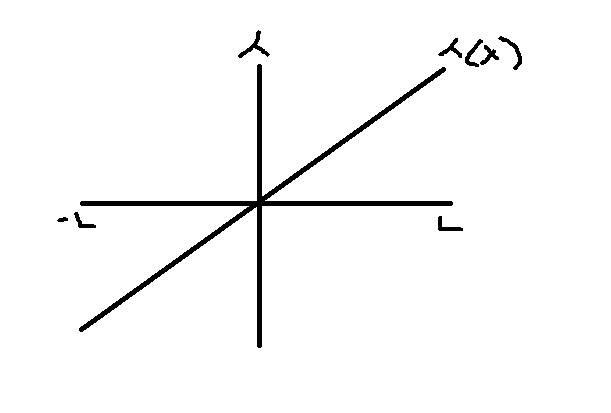
graph charge density as a function of x from -L to L would just look like this because using the values and plugging it into the lambda equation it would produce these values.
2.
To find the electric potential I first need to find the correct form of dq.
Using the lambda equation
λ = Q / 2L ,
since L = 2L ,
Q = λ2L , then for dq = λ2dl
then
V = k ∫ λ2dl / √(L/2)^2 + y^2 (bounds for integral is from 0 to 2L)
because r = √(L/2)^2 + y^2
then it integrates to
V = 2kλ [ln(y^2 + √(L/2)^2 + y^2] |2L to 0
V = 2kλ [ln(y^2 + √((2L/2)^2 + y^2 - ln(y^2 + √(0/2)^2 + y^2))]
V = 2kλ [ln(y^2 + √L^2 + y^2 - ln(y^2 + √y^2]
then using log rules,
V = 2kλ [ln (y^2 + √L^2 + y^2 ) / (y^2 + y)
is this so far correct? I need to make sure this is correct before I can continue
A thin rod of length 2L has charge Q uniformly distributed along its length.
1. Draw a graph of the charge density as a function of x from -L to L
2. Find the electric potential at point P a distance y away
3. Use the result in part 2 of the electric field at point P (you are finding the electric field as a function of a y equation)
4. Assess ; Draw the V versus y graph and draw the E versus y graph.
2. Known equations
v = k ∫ dq / r
e = -∇v
λ = Q / L
3. Attempt
1.
graph charge density as a function of x from -L to L would just look like this because using the values and plugging it into the lambda equation it would produce these values.
2.
To find the electric potential I first need to find the correct form of dq.
Using the lambda equation
λ = Q / 2L ,
since L = 2L ,
Q = λ2L , then for dq = λ2dl
then
V = k ∫ λ2dl / √(L/2)^2 + y^2 (bounds for integral is from 0 to 2L)
because r = √(L/2)^2 + y^2
then it integrates to
V = 2kλ [ln(y^2 + √(L/2)^2 + y^2] |2L to 0
V = 2kλ [ln(y^2 + √((2L/2)^2 + y^2 - ln(y^2 + √(0/2)^2 + y^2))]
V = 2kλ [ln(y^2 + √L^2 + y^2 - ln(y^2 + √y^2]
then using log rules,
V = 2kλ [ln (y^2 + √L^2 + y^2 ) / (y^2 + y)
is this so far correct? I need to make sure this is correct before I can continue