Electron deflection in a cathode ray tube

[pcandrepair]

Homework Statement

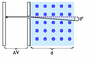
An electron in a cathode ray tube is accelerated through a potential difference of ΔV = 11 kV, then passes through the d = 4 cm wide region of uniform magnetic field. What field strength (in mT) will deflect the electron by 10(degrees)? (Hint: is it a reasonable approximation to treat the magnetic force on the electron as being in a constant direction?)

Homework Equations

F(B) = qvB

v = \sqrt{(-2*e*V/Mass(e))}

The Attempt at a Solution

Using the equation for velocity, I found that the velocity of the electron when leaving the "accelerator" has a velocity of v = 6.21601628 x10^7 m/s

I also found that the electron is deflected .007053m down when passing through the magnetic field.

I'm not sure where to go from here... Would I find the force of the magnetic field, (F(B)), and then find the magnitude of B using the equation given above? If so, how would I do this? Thanks for any help!

 

[nothing123]

Anyone figure this out?

Just off of your attempt, you could proceed by finding how much time it takes to cross the 4cm wide magnetic field using the initial velocity. With this time, you could calculate the vertical acceleration downwards. Then, use F=ma to find the magnetic force and finally F=qvB to find the magnetic field. I also have this question in my textbook but using this method, I can't get the exact answer.

 

[EngageEngage]

The force direction isn't constant like the hint says because as the electron starts turning, so does the direction of force. So, the electron will start spinning in a circle (if the walls weren't there) whose radius is given by the following equation-- qvB = mv^2/r. You know that the radius should intersect the right wall at the requested point of collision. From this you should be able to solve the problem I would think.

 

[nothing123]

Would the radius calculation be: omega = 10degrees/time = v/r?

 

[EngageEngage]

i'm not sure how you got there and am not sure if its right or wrong, but here is how i would to it: You already have one triangle on the given picture. Find the hypotenuse of that trinagle. Then you can draw in another triangle whose vertex is the center of the circle and who's legs are both the radius r, and the far side is the hypotenuse of the smaller triangle. One of the legs will lie along the left wall and will connect to the vertex of the smaller triangle. The second leg will extend to the collision point on the opposite wall, once again connecting to the end of the hypotenuse of the smaller triangle. With some simple trig you should be able to find the answer pretty quickly for r. then you could take this answer, and plug it into your equation B = mv/rq and see if its right.

 

[nothing123]

I'm not sure what you're getting at but essentially my equation is using circular motion. Angular velocity (omega) = change in radians (10deg in radians)/time (which was found using the horizontal velocity across the 4cm width magnetic field). Angular velocity is then just the velocity/radius. I think I got something like 0.115m for the radius which worked out the correct answer.

 

[damionpitt]

http://www.cramster.com/answers-jul-09/physics/field-strength-an-electron-in-a-cathode-ray-tube-is-accelerated-through-a_620772.aspx


this is kinda like this problem. see if it helps any.

 

[DivJun93]

When was this written, in i think year 2008?
Well, new to this blog, i know the answer.

To the person who asked the question we know E=F/Q and we also know that E=v/d. combine the equations together to get the value of the force. i.e- we know Q is charge of electron, v is the velocity you had calculated, and d is 4cm (convert to metres).
So now we have the value of F. and we know that F=BQv... hence find value of B.. whereby we know the value of F, and Q is charge of electron and v was the speed. and then you get your value of B... then obviously use simple algebra to convert it to mega or milli Tesla..

Hope that helps after the two years!