Solve Cyclotron Motion Homework

In summary, an electron in a cathode-ray tube is accelerated through a potential difference of 10 kV and then enters a region of uniform magnetic field with a width of 2.4 cm. Using the equations for circular motion and knowing the initial velocity and potential difference, we can calculate the radius of the electron's path as 10.669 cm. Solving for the magnetic field gives a value of 4.1 * 10^-7 T, but this result was found to be incorrect. The angle theta for the tangent at the exit point was found to be 15°.
  • #1
solzonmars
10
0

Homework Statement


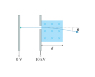
An electron in a cathode-ray tube is accelerated through a potential difference of 10 kV, then passes through the d = 2.4-cm-wide region of uniform magnetic field in the figure.
33.P59.jpg


Homework Equations


- Am I taking the entirely wrong approach in the solution?

The Attempt at a Solution


Since this is circular motion, we can draw a circle which intersects the square in the picture at where the electron exits the cathode ray tubes and the place it exits the square. Geometry then gives the angle between the tangent to the latter point and the hypotenuse, and we find that the radius is 10.669 cm. We could then use mv^2/R = qvB, and we know that 1/2mv^2 = q*10000 from the cathode ray tube. Solving for B gives B = 4.1 * 10^-7 T, which is incorrect.
 

Attachments

  • 33.P59.jpg
    33.P59.jpg
    3.7 KB · Views: 567
Physics news on Phys.org
  • #2
What is the angle theta?
It's not given in your question, how did you calculate the radius?
 
  • #3
I didn't realize it wasn't given in the figure. Theta is 15°.
 

1. What is cyclotron motion?

Cyclotron motion is the circular motion of a charged particle in a uniform magnetic field. The particle moves in a circular path due to the Lorentz force, which is the force experienced by a charged particle in a magnetic field.

2. How is cyclotron motion used in science?

Cyclotron motion is used in a variety of scientific applications, such as particle accelerators, mass spectrometry, and medical imaging. It allows scientists to manipulate and study the behavior of charged particles in a controlled manner.

3. What is the equation for cyclotron motion?

The equation for cyclotron motion is given by F = qvB, where F is the Lorentz force, q is the charge of the particle, v is its velocity, and B is the magnetic field strength. This equation can also be written as ma = qvB, where m is the mass of the particle and a is its acceleration.

4. What factors affect the motion of a particle in a cyclotron?

The motion of a particle in a cyclotron is affected by several factors, including the strength of the magnetic field, the charge and mass of the particle, and the initial velocity of the particle. The radius of the particle's path is also affected by these factors, as well as the frequency and strength of the alternating electric field used to accelerate the particle.

5. How do you solve problems involving cyclotron motion?

To solve problems involving cyclotron motion, you will need to use the equations for the Lorentz force and centripetal force to determine the acceleration and radius of the particle's path. You may also need to use other equations depending on the specific problem, such as equations for energy or velocity. It is important to carefully analyze the given information and assign appropriate values to variables before solving the problem.

Similar threads

Understanding Fundamentals of Electronics: Solving an Electric Charge Problem
    • Introductory Physics Homework Help
Replies
11
Views
1K
Calculate the deflection sensitivity in mm per volt
    • Introductory Physics Homework Help
2
Replies
44
Views
10K
Electrons in a cathode ray tube
    • Introductory Physics Homework Help
Replies
4
Views
1K
Solve Cyclotron Question: Calculate Magnetic Field & Time to Exit
    • Introductory Physics Homework Help
Replies
6
Views
6K
Cathode Ray Tube and magnetic field Question
    • Introductory Physics Homework Help
Replies
1
Views
2K
Energy inside a cyclotron, and the frequency of circular motion
    • Introductory Physics Homework Help
Replies
2
Views
2K
Field strength to deflect electron in a cathode-ray tube
    • Introductory Physics Homework Help
Replies
16
Views
7K
Finding constant acceleration without time
    • Introductory Physics Homework Help
Replies
3
Views
14K
Confused about derivation of E=(V-IR)/L, multiple choice problem
    • Introductory Physics Homework Help
Replies
3
Views
3K
Electric potential difference?
    • Introductory Physics Homework Help
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top