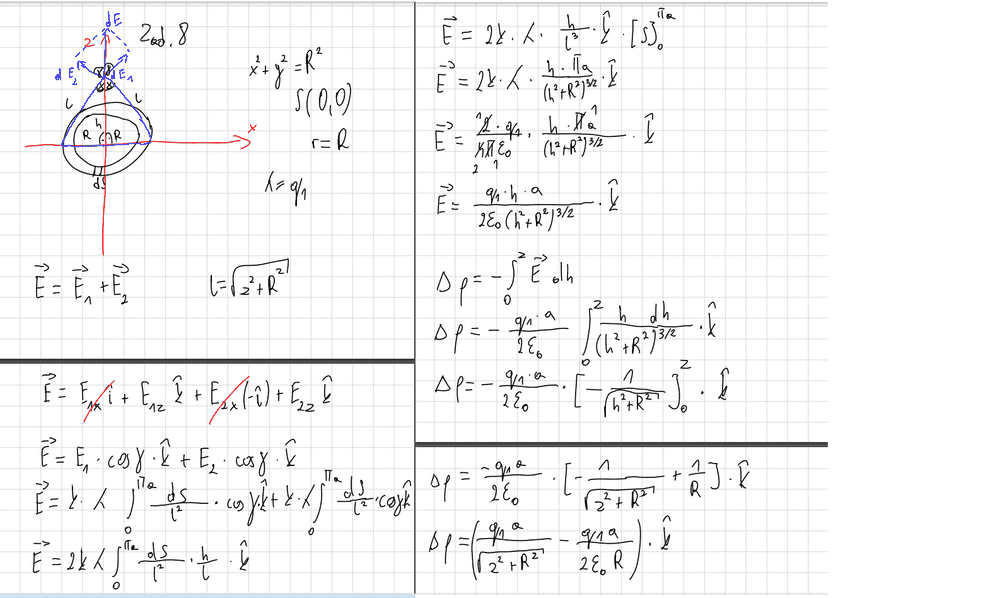SUMMARY
The discussion focuses on calculating the electric field near a charged ring using integration techniques. Participants emphasize the importance of using LaTeX for clarity in presenting equations. The correct approach involves integrating the potential from an infinitesimal segment around the ring rather than using the more complex method of integrating from infinity. The total potential is additive, which simplifies the calculations significantly.
PREREQUISITES
- Understanding of electric fields and potentials
- Familiarity with cylindrical coordinates
- Proficiency in calculus, specifically integration techniques
- Knowledge of LaTeX for formatting mathematical expressions
NEXT STEPS
- Study the integration of electric fields in cylindrical coordinates
- Learn how to apply the principle of superposition in electrostatics
- Explore the use of LaTeX for writing complex equations
- Investigate the relationship between electric potential and electric field
USEFUL FOR
Students and professionals in physics, particularly those studying electrostatics, as well as educators looking to enhance their teaching methods with clear mathematical presentation.