gruba
- 203
- 1
Homework Statement
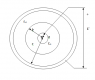
Spherical capacitor with two linear and uniform dielectrics with relative permitivitty Ɛr1 and Ɛr2 is connected to constant voltage U. When second dielectric is removed, intensity of electric field by inner electrode is reduced by 1/3, and electric field by outer electrode is increased two times. a=1.5mm, b=6mm, c=12mm. Calculate Ɛr1 and Ɛr2.
Homework Equations
Gauss law
The Attempt at a Solution
In the first case (two dielectrics), Gauss law gives E_1^{(1)}=\frac{Q}{4\pi\epsilon_0\epsilon_{r1}r^2},a<r<b
E_2^{(1)}=\frac{Q}{4\pi\epsilon_0\epsilon_{r2}r^2},b<r<c
U^{(1)}=\int_a^b \frac{Q}{4\pi\epsilon_0\epsilon_{r1}r^2}\mathrm dr+ \int_b^c \frac{Q}{4\pi\epsilon_0\epsilon_{r2}r^2}\mathrm dr=\frac{Q}{4\pi\epsilon_0}\left(\frac{b-a}{\epsilon_{r1}ab}+\frac{c-b}{\epsilon_{r2}bc}\right)
In the second case (second dielectric is removed),
E_1^{(2)}=\frac{Q}{12\pi\epsilon_0\epsilon_{r1}r^2}
E_2^{(2)}=\frac{Q}{2\pi\epsilon_0r^2}
U^{(2)}=\frac{Q}{2\pi\epsilon_0}\left(\frac{b-a}{\epsilon_{r1}ab}+\frac{c-b}{bc}\right)
E_1^{(2)}=\frac{1}{3}\times E_1^{(1)}\Rightarrow \frac{Q^{(2)}}{4\pi\epsilon_0\epsilon_{r1}r^2} = \frac{1}{3}\frac{Q^{(1)}}{4\pi\epsilon_0\epsilon_{r1}r^2}\Rightarrow Q^{(2)}=\frac{Q^{(1)}}{3}
E_2^{(2)}=2\times E_2^{(1)}
\frac{Q^{(2)}}{4\pi\epsilon_0 r^2} = 2\frac{Q^{(1)}}{4\pi\epsilon_0\epsilon_{r2} r^2}
From these equations, I get that \epsilon_{r2}=6
U^{(1)}=\int_a^b \frac{Q}{4\pi\epsilon_0\epsilon_{r1}r^2}\mathrm dr+ \int_b^c \frac{Q}{4\pi\epsilon_0\epsilon_{r2}r^2}\mathrm dr=\frac{Q^{(1)}}{4\pi\epsilon_0}\left(\frac{b-a}{\epsilon_{r1}ab}+\frac{c-b}{\epsilon_{r2}bc}\right)
U^{(2)}=\frac{Q^{(2)}}{4\pi\epsilon_0}\left(\frac{b-a}{\epsilon_{r1}ab}+\frac{c-b}{bc}\right)
U^{(1)}=U^{(2)}\Rightarrow \epsilon_{r1}=36017.1
In my book's solution \epsilon_{r2}=3 and \epsilon_{r1}=6
Could someone please check this?