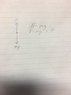TheFlemster
- 25
- 0
Homework Statement
A 74.0 kg person is standing inside an elevator. The elevator is moving from the 3rd floor to the 21st floor. As the elevator passes the 4th floor it is moving at 2.30 m/s and is increasing speed at a rate of 1.43 m/s2 . At this moment, what is the normal force that acts on the person?
Homework Equations
normal Force, N = m(a+g)
F = ma
The Attempt at a Solution
The attempt at solution is on the attached image. Am I working it correct or should I have used F=ma?