Elliot Wave Structure: Predicting Market Vibrations

[aricho]

suppose the "elliot wave structure" and movement in markets is fact and causes a vibration everytime (a vibration is a change in price due to a factor, here being the range).

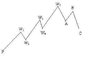
The elliot wave structure says that markets move in 5 waves as shown below, one up, one down ect till the top, where an ABC happens (not all the time, but suppose that for now).

sometimes you can predict a vibration by using the range and fractions of it on the way down, and you can predict a target by using 1+ the fraction.

An example of this is in the 2nd picture where the market bounces off the 1/4 retracement (3/4 of the range from the bottom, 1/4 from the top.)

We can look at trends over many different time frames. Now look at C as the low, instead of A.

Is this equation valid?

{c} = \frac{x}{y}\times{r} + {p}

that was the first time I've ever done one of those so if it doesn't work i'll try it again.

in the equation, \frac{x}{y} is either 1/2, 1/3, 2/3, 1/4, 3/4, 3/8, 5/8 or 7/8. As you see this would make many different prices.
r is the range between the top of wave 5 (w5) and P.
the result is added to P to give the level (price) of the vibration.

This just happened recently, where the market had a low of 3927 and a high of 4322. The range was 4322-3927=395. So a one quarter vibration is 3/4 X 385 + 3927=4223 (EXACT VIBRATION) (S&P200 aussie)

could the above formula be used to produce vibration levels? or is there a better equation?

Thanks

 

[Curious3141]

I quickly grew disillusioned with Technical Analysis (which includes Elliot Waves, Fibonacci series ("Fibs"), Support and Resistance Levels, EMAs, MACD, Candlestick charting, etc. etc.)

The so called pundits frequently fail to make any intelligible clear analysis of the data. And even in the event that they do make a prediction about a trend or support/resistance levels, they will always hedge their predictions by saying rubbish like "wait for the market to give a clear signal by breaking the levels or establishing a clear trend before committing yourself". This is highly unscientific. There is no testable prediction, because they're constantly second guessing themselves ! And when the market does make a clear and decisive move in a certain direction, you don't really need all this mumo jumbo anyway, the trend is self evident.

"Professional" "Ellioticians" talk about verifying Elliot wave counts. This is because they're NEVER sure about what to make of that little squiggle in a real life graph, whether it's actually a wave 1, a wave 3, a 5, or whatever.

I've come to regard the whole thing as so much snake oil. I guess charlatans and wishful thinkers abound everywhere, including the financial world.

 

[aricho]

yer i know

it is a load of rubbish most of the time, but i was just "curious" to see if the formula i made up was actally valid... what do you reckon?