Energy of a Dipole in a Uniform E Field

[dunna]

Homework Statement

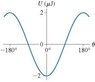
The graph shows the potential energy of an electric dipole which is in a constant electric field; only the electric force is acting on the dipole. Consider a dipole that oscillates between +/- 51 degrees.

What is the dipole's kinetic energy when it is aligned with the electric field?

Homework Equations

Known: At 180, U= 2*10^-6 J

The Attempt at a Solution

In a previous section, the mechanical energy was asked for. Using U=pEcos(theta), I put substituted U=2.0*10^-6, theta=180degrees, and kept pE constant. pE was calculated to be -2.0*10^-6 J, then reworked the problem with a theta=51degrees to find the mechanical energy= -1.26*10^-6 J.

My understanding is that when the dipole is aligned with the Electric Field, the theta between them is zero and this is the potential energy's lowest value. I figure that the potential energy's lowest value would correlate with the kinetic energy's highest value and the answer would be 2.0*10^-6. This is incorrect. Also tried -2.0, 0, 1.26, -1.26, and -4 all *10^-6.

I have the problem wrong using all my attempts, but what is logic to figuring it out?

 

[ehild]

The dipole oscillates betwen +/- 51 degrees. It never reaches 180 degree. What is the KE and potential energy at the maximum deviation from the direction of the electric field?

 

[dunna]

I found the maximum potential energy to be 1.26*10^-6 J at 51degrees

 

[ehild]

Take care, the energy of the dipole is -pEcos(θ). At 51°, it is -1.26*10^-6 J. As the KE is zero there, the total energy of the oscillating dipole is -1.26*10^-6 J. The potential energy of the dipole when aligned with the field is -pEcos(θ) = -2.0*10^-6 J, opposite to the energy at θ=180 degree. If the total energy is -1.26*10^-6 J and the potential energy is -2.0*10^-6 J, how much is the kinetic energy?

ehild