JrK
- 139
- 1
I use an example with a rack and a pinion. I suppose there is no losses from friction. I suppose the masses very low to simplify the study, and there is no acceleration. I suppose the tooth of the pinion and the rack perfect, I mean there is no gap. There is always the contact between the rack and the pinion, I mean the tooth are always in contact.
The device:
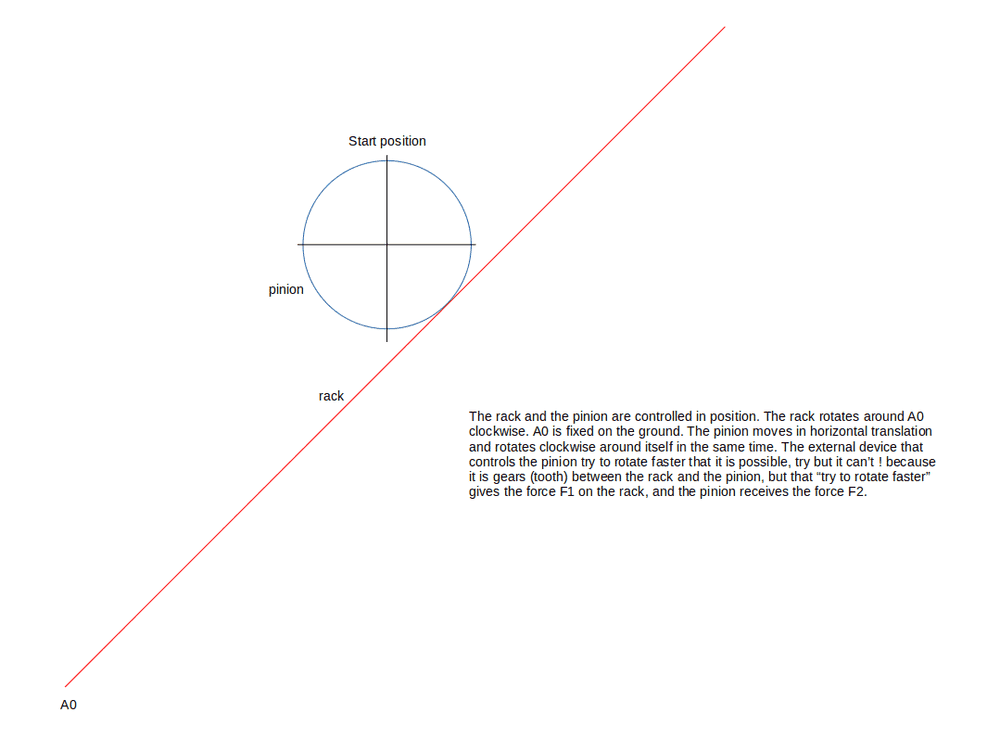
I drew 2 positions:
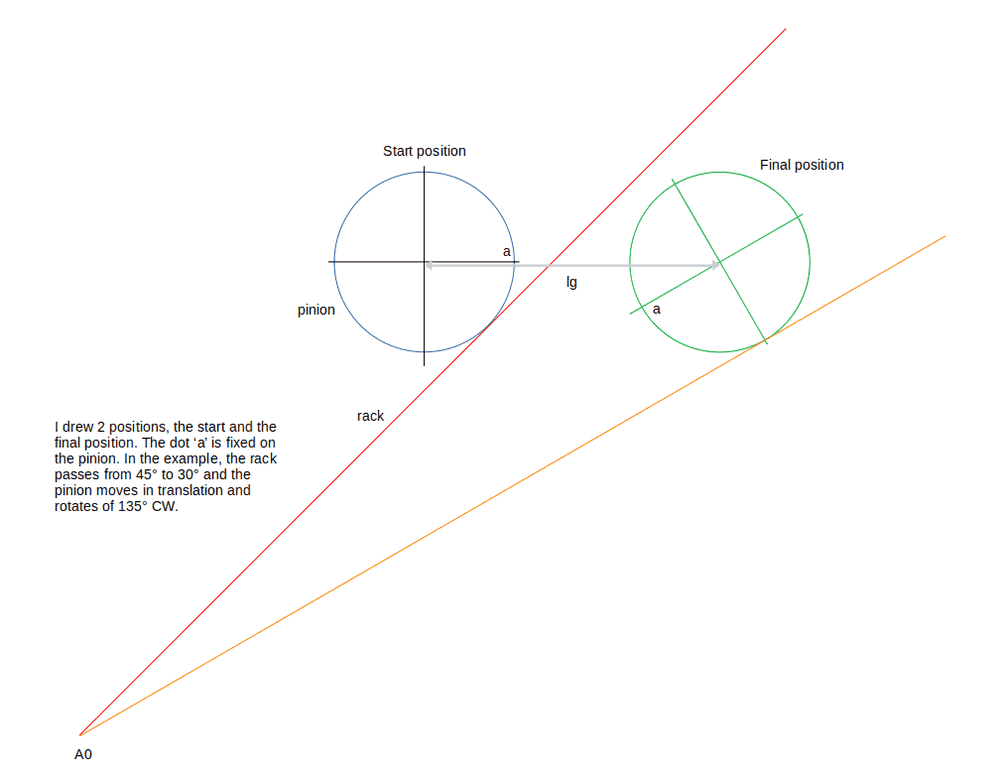
The distance lg equal to 131 mm.
Because the pinion tries to rotate faster there are the force F1 on the rack and the force F2 on the pinion:
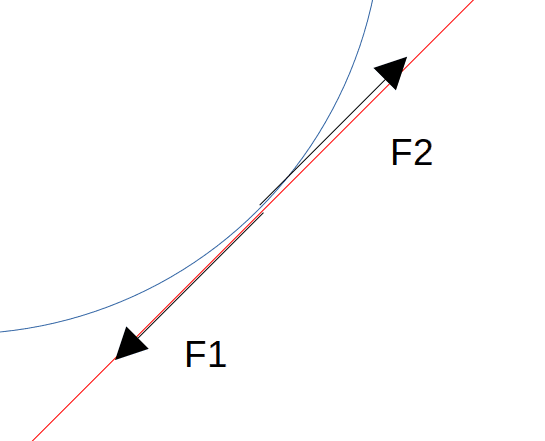
I suppose the force F1 and F2 constant in value for the calculation, the value of F1 = the value of F2 = 1 N for example. The value of F1 is equal to the value of F2. The orientation of the forces F1 and F2 have the orientation of the red wall.
I used a geometric method to measure the distance of rotation needed for the pinion (around itself):
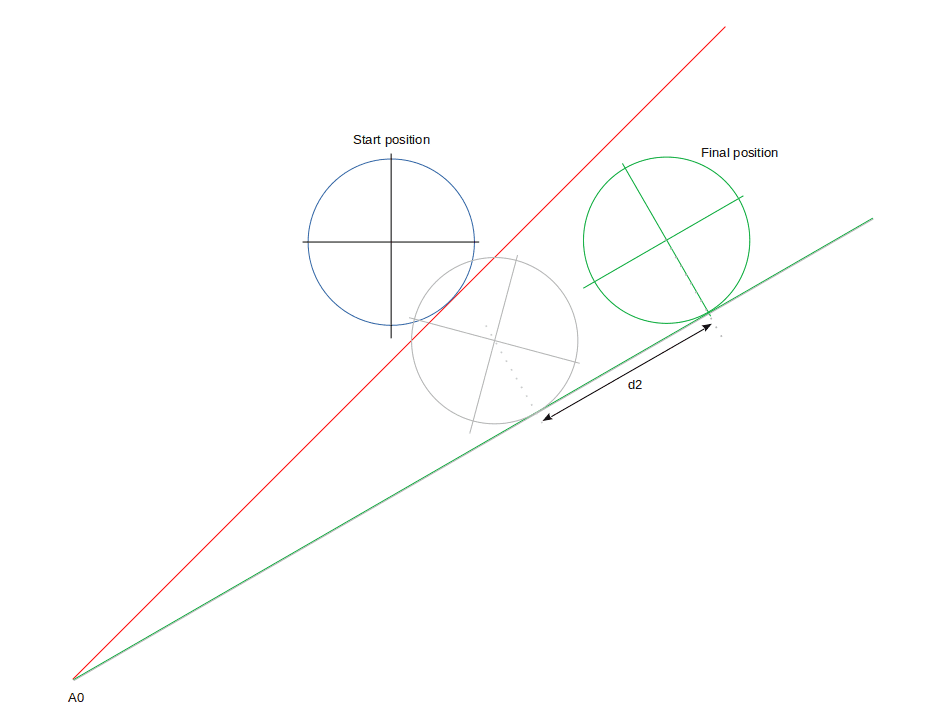
I measured d2=94 mm. So the energy needed to rotate the pinion is d2*F1 = 94*1= 94 J. The energy needed to move the pinion in translation is lg*(sin(pi/4)-sin(pi/6))/(pi/12) = 103 J.
So maybe the distance d2 is not like I think ? or the integral is not correct ?
I used a program to measured the length d2 and lg and the energies:
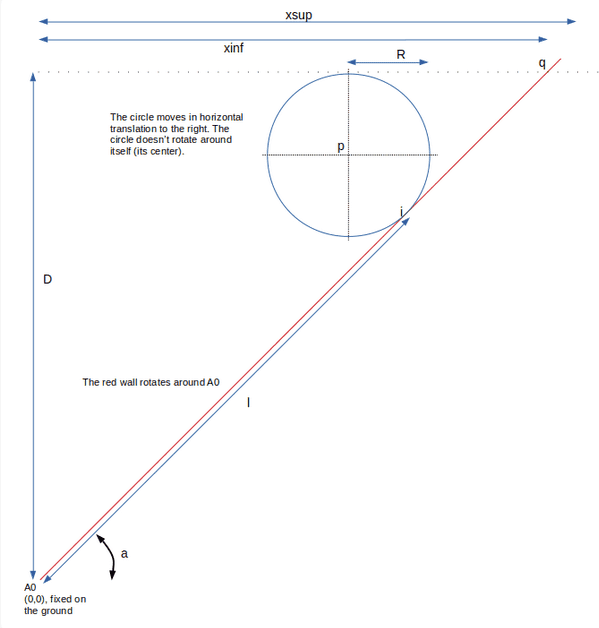
And the notations:
The device:
I drew 2 positions:
The distance lg equal to 131 mm.
Because the pinion tries to rotate faster there are the force F1 on the rack and the force F2 on the pinion:
I suppose the force F1 and F2 constant in value for the calculation, the value of F1 = the value of F2 = 1 N for example. The value of F1 is equal to the value of F2. The orientation of the forces F1 and F2 have the orientation of the red wall.
I used a geometric method to measure the distance of rotation needed for the pinion (around itself):
I measured d2=94 mm. So the energy needed to rotate the pinion is d2*F1 = 94*1= 94 J. The energy needed to move the pinion in translation is lg*(sin(pi/4)-sin(pi/6))/(pi/12) = 103 J.
So maybe the distance d2 is not like I think ? or the integral is not correct ?
I used a program to measured the length d2 and lg and the energies:
Code:
#include <stdio.h>
#include <math.h>
int main()
{
long double pi=M_PI;
long int N=10000000L;
long double R=.1;
long double D=1.;
long double xinf=1;
long double xsup=xinf/tanl(44.99/180.0*pi);
long double px1=0,py1=0,a1=0,px2=0,py2=0,a2=0,dl=0,wrotation=0,wtranslation=0,ix1=0;
long double iy1=0,ix2=0,iy2=0,qx1=0,qy1=0,s=0,xl1=0,yl1=0,xl2=0,yl2=0;
long double sx=0,sy=0,qx2=0,qy2=0,suma=0,l=0,asav=0;
long double xf=0,yf=0,wp=0,af=0,dlrc=0,dlpc=0;
long int i;
qy1=D;
py1=qy1-R;
for(i=0;i<N;i++)
{
qx1=xinf+(xsup-xinf)/N*i;
a1=atanl(qy1/qx1); if(i==0) a2=a1;
s=R/tanl(a1/2.);
px1=qx1-s;
ix1=px1+R*sinl(a1);
iy1=py1-R*cosl(a1);
if(i>0)
{
l=(sqrtl(ix1*ix1+iy1*iy1)+sqrtl(ix2*ix2+iy2*iy2))/2.;
xf=ix2+l*sinl(a1)*fabsl(a2-a1);
yf=iy2-l*cosl(a1)*fabsl(a2-a1);
af=fabsl(atanl((iy1-yf)/(ix1-xf)));
wtranslation+=fabsl(px2-px1)*cosl((a1+a2)/2);
wrotation+=sqrtl((ix1-xf)*(ix1-xf)+(iy1-yf)*(iy1-yf))*cos(a1-af);
}
px2=px1; py2=py1; qx2=qx1; qy2=qy1; ix2=ix1; iy2=iy1; xl2=xl1; yl2=yl1; a2=a1;
}
printf("\nN=%ld , R=%Lf , D=%Lf , xinf=%Lf , xsup=%Lf",N,R,D,xinf,xsup);
printf("\nwtranslation=%Lf , wrotation=%Lf\n",wtranslation,wrotation);
return 0;
}And the notations: