lat77
- 6
- 0
Homework Statement
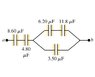
For the capacitor network shown in the Figure (Figure 1) , the potential difference across is 12.0 . (Figure is attached by the way)
A)Find the total energy stored in this network. (I already found this to be 158 μJ)
B)Find the energy stored in the 4.80- capacitor.
Homework Equations
U=1/2 CV^2
The Attempt at a Solution
I would imagine that you need to subtract the amount of energy in the parallel branches from the total amount of energy of the system, but I don't know how to do this without knowing the charge.