tgrandahl
- 3
- 0
Hello,
I have recently found an urge to understand the amount of energy that I use while driving.
I would like to be able to record tracking data via GPS in a GPX format, and then calculate the amount of energy that would be used to perform the same trip using various vehicle models.
I would also like to be able to realize the energy that may be rescued using regenerative braking in an electric vehicle or hybrid.
I have started working on this in an excel worksheet because I feel it will be easiest to layout the math necessary to estimate the energy used. The worksheet currently calculates force for acceleration, normal force, and drag.
Over my 7.1 mile journey I used:
710171 J accelerating,
1614412.8 J fighting normal force,
17182665 J fighting drag... Seriousley ?...
I wanted to have some control value to compare my calculations with to know if I am on track or not.
~7.1 mile trip,
~23 MPG,
~132x10^6 J / gallon of gasoline,
~12% of consumed energy reaches the wheels of my vehicle
(7.1/23)*132x10^6*0.12 = 48.9x10^4 J
My worksheet currently calculates 19.5x10^5 J being used
Although my vehicle is consuming roughly 40.7x10^5 J in gasoline during the drive my vehicle would have to be 50% efficient!
On top of that I am currently being very generous and not summing the energy used while going downhill even for the drag. Looking at the numbers it seems as if my error is in my drag calculation.
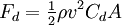
W=FxD
I am using the typical drag coefficient and p values gamesguru listed here:
https://www.physicsforums.com/showthread.php?t=246885"
The actual weight of my vehicle, 1584Kg.
I do understand the resolution of my GPS data is rather poor. It was collected using my iphone during a quick trip. I need allot more points and more accurate altitude. However I did expect to be able to get some sensible results from it.
I wouldn't say physics is one of my real strengths so I am hoping this is a simple error. Can anyone here show me where I have steered off course? I have attached the worksheet, thank you for any help you can provide.
~Tyler Grandahl
I have recently found an urge to understand the amount of energy that I use while driving.
I would like to be able to record tracking data via GPS in a GPX format, and then calculate the amount of energy that would be used to perform the same trip using various vehicle models.
I would also like to be able to realize the energy that may be rescued using regenerative braking in an electric vehicle or hybrid.
I have started working on this in an excel worksheet because I feel it will be easiest to layout the math necessary to estimate the energy used. The worksheet currently calculates force for acceleration, normal force, and drag.
Over my 7.1 mile journey I used:
710171 J accelerating,
1614412.8 J fighting normal force,
17182665 J fighting drag... Seriousley ?...
I wanted to have some control value to compare my calculations with to know if I am on track or not.
~7.1 mile trip,
~23 MPG,
~132x10^6 J / gallon of gasoline,
~12% of consumed energy reaches the wheels of my vehicle
(7.1/23)*132x10^6*0.12 = 48.9x10^4 J
My worksheet currently calculates 19.5x10^5 J being used
Although my vehicle is consuming roughly 40.7x10^5 J in gasoline during the drive my vehicle would have to be 50% efficient!
On top of that I am currently being very generous and not summing the energy used while going downhill even for the drag. Looking at the numbers it seems as if my error is in my drag calculation.
W=FxD
I am using the typical drag coefficient and p values gamesguru listed here:
https://www.physicsforums.com/showthread.php?t=246885"
The actual weight of my vehicle, 1584Kg.
I do understand the resolution of my GPS data is rather poor. It was collected using my iphone during a quick trip. I need allot more points and more accurate altitude. However I did expect to be able to get some sensible results from it.
I wouldn't say physics is one of my real strengths so I am hoping this is a simple error. Can anyone here show me where I have steered off course? I have attached the worksheet, thank you for any help you can provide.
~Tyler Grandahl
Attachments
Last edited by a moderator: