Energy when Force is perpendiclar to direction of movement

[jt-walsh]

Hello everyone, I made a problem where a shuttle travels to the moon the mine deuterium to fuse on earth, I started incredibly simplistic and I'm working my way up. At first I had the moon static, but now I have the moon moving at a constant radius and constant velocity. I have the shuttle move in a straight line to the moon. Ripping the vectors to calculate the force wasn't to difficult, neither was calculating the energy to over come wind resistance, gravity, to accelerate and jerk in the y direction, but I haven't been able to calculate the energy needed to hold shuttle static in the x-direction.

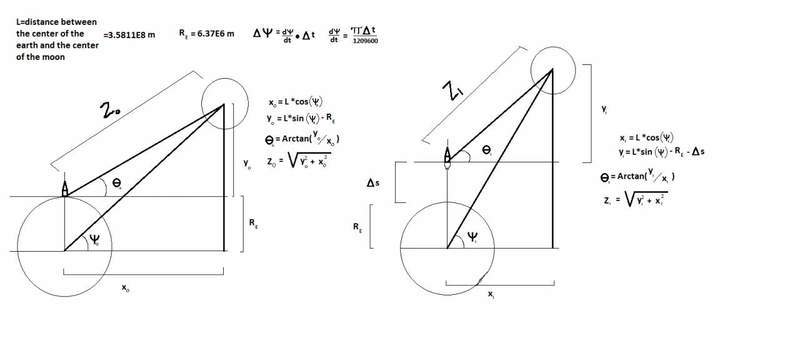Here's a pretty picture I drew to illustrate the problem.

The force due to gravity in the y direction would be the 5.97E24*1E5*G/(6.37E6+Δs)-sin(θ)*7.35E22*G*1E5/z²

The force due to gravity in the x direction would be cos(θ)*7.35E22*1E5*G /z²

z would be the distance between the center of gravity of the moon and the shuttle, 5.97E24 is the mass of the Earth in kg, 7.35E22 is the mass of the moon. The mass of the shuttle would be 100,00 kg

I'm wondering if there's a way to solve for the energy needed if the shuttle travels in a straight line or if I definitely need to make it so that shuttle travels a curved path. (I plan to make it that way later, but right now I'm trying to solve for other things but i want to get this first).

If anyone wants I can give what ψ0 equals, the position equations and other relevant equations.

*edit* apologies, I forgot to factor in the mass of the shuttle and gravitational constant int he force equations.

 

[rcgldr]

I haven't been able to calculate the energy needed to hold shuttle static in the x-direction.

The only external (to the shuttle) force in the x direction is gravity from the moon. This will get complicated because the moon and shuttle are moving and accelerating and the force is relative to G M_moon M_shuttle / distance².

Using a curved path will take much less energy. Once outside the atmosphere, it most efficient to minimize the force used against gravity, so thrust should be perpendicular to gravity (velocity will be an outwards spiral due to the increase in velocity). It's also more efficient to minimize the duration of each thrust impulse.

 

[jt-walsh]

I know using a curved path would be more efficient, but I'm trying to focus on other aspects of the problem, but I can't just leave that part unsolved, and if I changed it I would have to change everything I've already done. However, if it proves too complicated to solve the way I wrote it up I'll have to do that.

Oh, and sorry I forgot to factor in the mass of shuttle and the gravitational constant, I factored them and forgot to put them back in :/