Equating Voltage/Current of Associated Sources: A Comprehensive Guide

[Jhenrique]

How equate the voltage/current of the associated sources with the voltage/current equivalent?

 

[Drakkith]

For voltage sources in series, simply add the voltages up. In parallel, the voltage of the circuit is the same as any single source, but each source will have a fraction of the total current. So if you have three 9-volt batteries in parallel, there's 9 volts applied to the circuit and each battery supplies 1/3 of the total current.

For current sources it's the opposite. The current through each current source in series is the same, while you would add the current sources together if they are in parallel.

 

[jbriggs444]

In parallel, the voltage of the circuit is the same as any single source, but each source will have a fraction of the total current. So if you have three 9-volt batteries in parallel, there's 9 volts applied to the circuit and each battery supplies 1/3 of the total current.

The parallel situation is not quite this simple. For ideal sources of equal voltage connected in parallel by ideal wires there is no guarantee that each supplies 1/3 of the total current. Any combination adding up to 1 will satisfy the relevant equations. For ideal sources of unequal voltage connected in parallel by ideal wires, there is no way to satisfy the relevant equations.

For near-ideal sources, connected in parallel, small details matter. If the sources have equal voltage then the current will be distributed based on the (small) internal resistance in each source and in the connecting wires. If the sources have unequal voltage than there will be large currents as the high voltage sources run current backwards through the low voltage sources. The result is a kind of averaging of the voltages of the component sources. The currents will become as large as is needed to prevent the voltage sources from behaving in an ideal fashion. The result is that the voltage of the parallel combination is some sort of average of the [nominal] voltages of the individual sources.

For current sources it's the opposite. The current through each current source in series is the same, while you would add the current sources together if they are in parallel.

Similar caveats apply for current sources. Perfectly ideal current sources connected in series must have equal values. Any other choice will fail. Near-ideal current sources connected in series will have extremely high potential differences created as the conflicts result in the accumulation or depletion of charge in the connections between. These voltage differences will become as large as is needed to prevent the current sources from behaving in an ideal fashion. The result is that the current through a series of current sources is some sort of average of the [nominal] currents of the individual sources.

Edit: Added the word "nominal" for a bit of clarity.

 

[Drakkith]

Ah, you are correct Jbriggs. I forgot to say that my explanation only applies when the voltage sources in parallel are equal in voltage and the current sources in series are equal in current.

 

[UltrafastPED]

In real life you don't want voltage sources in parallel, or current sources in series ... !

 

[Jhenrique]

I don't understand...

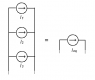
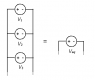
Yeah, I₁ ≠ I₂ ≠ I₃ so like V₁ ≠ V₂ ≠ V₃, and the sources are ideal.

I don't want to divide the total current/voltage for each source, I want that when given I₁, I₂ and I₃, or V₁, V₂ and V₃, find the I_eq and V_eq for every four cases above.

You're saying that this is impossible?

 

[jbriggs444]

I don't understand...

Yeah, I₁ ≠ I₂ ≠ I₃ so like V₁ ≠ V₂ ≠ V₃, and the sources are ideal.

I don't want to divide the total current/voltage for each source, I want that when given I₁, I₂ and I₃, or V₁, V₂ and V₃, find the I_eq and V_eq for every four cases above.

You're saying that this is impossible?

Yes. Cases 2 and 3 are impossible for ideal sources with unequal voltages/currents.

Cases 1 and 4 are trivial. Add the voltages or currents respectively.

 

[dauto]

Yes. Cases 2 and 3 are impossible for ideal sources with unequal voltages/currents.

Cases 1 and 4 are trivial. Add the voltages or currents respectively.

And if you use non-ideal sources in real circuits for cases 2 and 3 just to see what happens something really bad might happen like a short circuit that might damage equipment/start a fire. Hard to guess since it would depend on the particular design of the sources.

 

[Jhenrique]

Now I liked of the answers!

 

[Jhenrique]

Cases 1 and 4 are possible only if I₁ = I₂ = I₃ and V₁ = V₂ = V₃ ?

 

[CWatters]

Cases 1 and 4 are possible only if I₁ = I₂ = I₃ and V₁ = V₂ = V₃ ?

That should be... Cases 2 and 3 are only possible if...

 

[Jhenrique]

That should be... Cases 2 and 3 are only possible if...

what? 2 and 3 are absolutely impossibles!

 

[CWatters]

Looks like I misunderstood your post.

Case 1: Possible. V_eq=V₁+V₂+V₃ and I₁=I₂=I₃.

Case 2: Possible but only if V₁=V₂=V₃=V_eq. Not recommended in the real world

Case 3: Possible but only if I₁=I₂=I₃=I_eq. Not recommended in the real world.

Case 4: Possible. I_eq=I₁+I₂+I₃ and V₁=V₂=V₃

 

[CWatters]

Case 2 and 3 can be done in the real world but care is needed. An example of case 2 is jump starting a car by placing two batteries in parallel. This works because they are not ideal voltage sources (no such thing as an ideal voltage source in the real world).

 

[Jhenrique]

Looks like I misunderstood your post.

Case 1: Possible. V_eq=V₁+V₂+V₃ and I₁=I₂=I₃.

Case 2: Possible but only if V₁=V₂=V₃=V_eq. Not recommended in the real world

Case 3: Possible but only if I₁=I₂=I₃=I_eq. Not recommended in the real world.

Case 4: Possible. I_eq=I₁+I₂+I₃ and V₁=V₂=V₃

Good! Existe some book that gives those explanations too? Cause I never see...