person123
- 326
- 52
I derived an equation for the trajectory of a projectile. Given the height and distance of the projectile, and the initial velocity, it determines the initial angle. When plugging it into desmos, it seemed to make sense (https://www.desmos.com/calculator/pfylvs4tau), but I still can't be sure.
I first determined the vertex of the parabola. I knew two points of the parabola and the derivative at one of these points. This gave me the following:
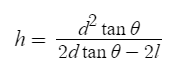
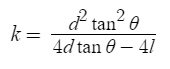
where d is the horizantal distance from the target, l is the vertical distance, and θ is the initial angle.
Since I knew the initial kinetic energy is the same is the product of the mass, acceleration due to gravity, and the height k, I was able to solve for the velocity v. By moving around the variables in this equation, it gave me
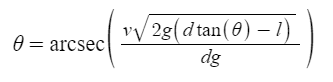
Does my method seem correct? Do the equations seem correct? (There's also the problem that I can't get theta completely to one side, although that's not really a physics problem).
I first determined the vertex of the parabola. I knew two points of the parabola and the derivative at one of these points. This gave me the following:
where d is the horizantal distance from the target, l is the vertical distance, and θ is the initial angle.
Since I knew the initial kinetic energy is the same is the product of the mass, acceleration due to gravity, and the height k, I was able to solve for the velocity v. By moving around the variables in this equation, it gave me
Does my method seem correct? Do the equations seem correct? (There's also the problem that I can't get theta completely to one side, although that's not really a physics problem).
Attachments
Last edited: