- #1
sbhatnagar
- 87
- 0
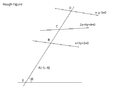
A line through \(A(-5,-4)\) meets the lines \(x+3y+2=0\), \(2x+y+4=0\) and \(x-y-5=0\) at the points \(B, \ C\) and \(D\) respectively. If
\[\left(\frac{15}{AB}\right)^2 + \left(\frac{10}{AC}\right)^2 = \left(\frac{6}{AD}\right) ^2 \]
, find the equation of the line.
\[\left(\frac{15}{AB}\right)^2 + \left(\frac{10}{AC}\right)^2 = \left(\frac{6}{AD}\right) ^2 \]
, find the equation of the line.