Equation of motion of a marble moving on a generic vertical guide

[Ovolollo]

Hello to everyone
I'd like to study this problem.

You have a 2D guide, described by an equation y = y (x) in a reference interval x ∈ I = [a, b], placed in a cartesian vertical plane Oxy.
The guide is frictionless and the only force that is acting is the gravity force.
On this track, a point like particle, e.g. a marble, is moving on the guide under the action of the gravity force from the point x = a to the point x = b, starting with null velocity.

Provided that the shape of the guide is allowing this motion, I would like to compute the time required to the marble to complete the path.

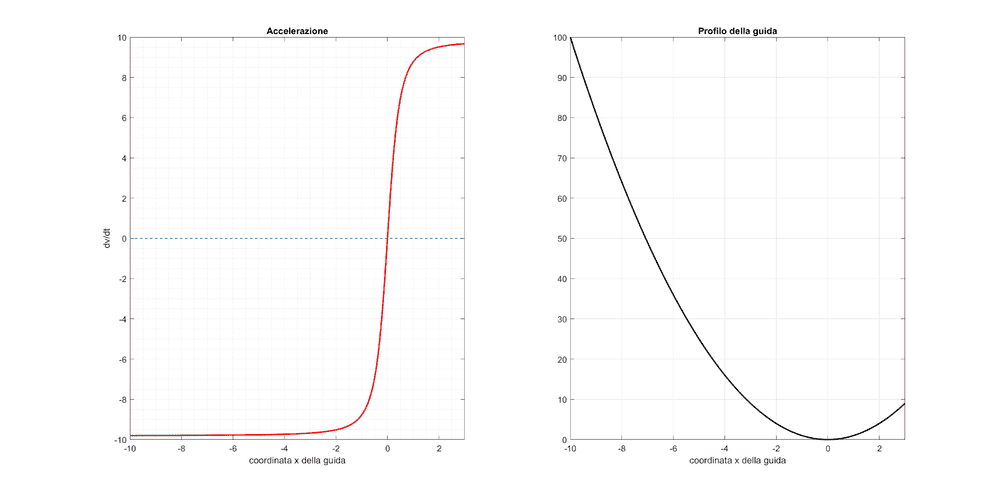
In the following picture I took a guide of equation y = x^2 and I've chosen an interval I = [-10, 3]. On the left picture you can see the tangential acceleration plotted against the x coordinate (as you can see in x = 0 no acceleration at all, while for big |x|, the tang. acceleration tends to become vertical so to the value 9.81), while on the right picture you can see the actual shape of the track y = y (x).

The tangential acceleration can be found with this equation (I'll skip how I got it):

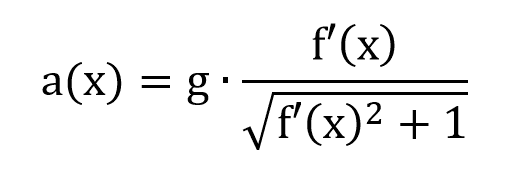
But then the problem that arises is how to link the coordinate x with the movement on the guide, called s. Suppose the marble moves 1 unit on the track, then you need to relate that motion to the guide x coordinate.
What I wrote was:

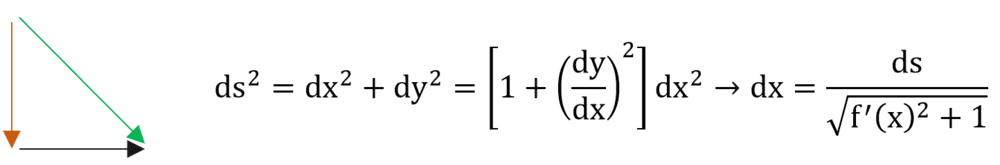
That is: the infinitesimal movement on the guide (green) is equal to the square root of the sum of the infinitesimal vertical movement squared, brown, and the infinitesimal horizontal movement squared, black.
So now I have a relationship between dx and ds.

Lastly, I've set up a numerical algorithm.

- Choose a dt (delta time).
- Compute tangential acceleration a, knowing the expression and the position x.
- Compute the speed v, as v = v_previous + a*dt.
- Compute the displacement along the guide s, as s = s_previous + abs(v*dt).
(the abs function states that the displacement on the guide is always increasing)
- Compute the corresponding x position, as x = x_previous + (s - s_previous) / sqrt (f'(x_previous)^2 + 1).
- Repeat while x <= b.

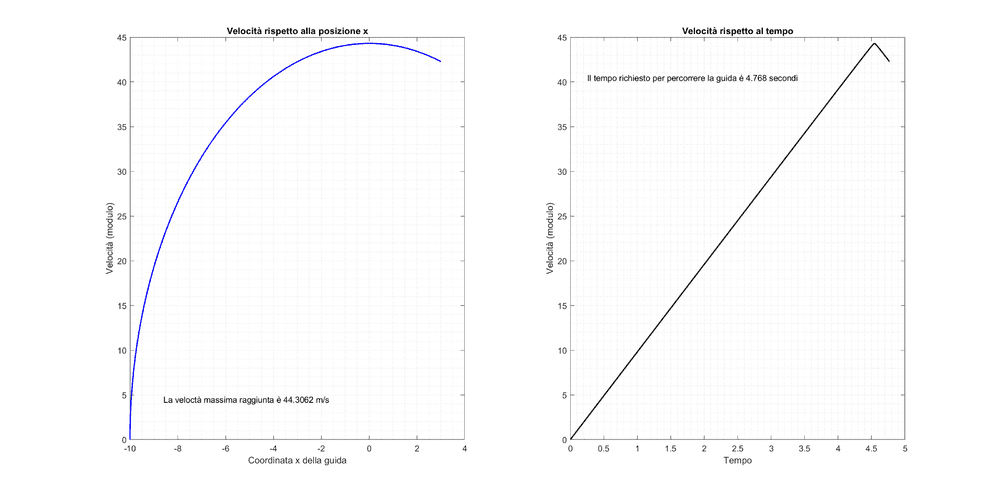
These are the results I have found for this specific problem (obtained for a dt = 0.001 seconds). On the left, a graph represents the velocity vs the x coordinate. The note says that the maximum reached speed is 44.3062 m/s and this is consistent with the well known equation of a falling object v = sqrt (2 g h), where h in this case, is the height at the point of maximum speed, i.e. 100 m.
On the right plot is depicted the speed against time. The time required to complete the path is 4.768 seconds and also this is quite consistent if you compare it to the time required for a body to free fall from 100 m to zero.

I would like to improve my algorithm and discuss with you about possible improvements in the theory behind it.
Thank you very much

 

[wrobel]

The equation of motion can be obtained by differentiating of the energy integral in time:
$$\frac{m}{2}|v|^2+mgf(x)=h,\quad |v|^2=\dot x^2+(f'(x)\dot x)^2.$$
There are a lot of standard tools for ode solving as well. Maple for example.

Summary:: To find the equation of motion of a point like particle (eg. marble) moving on a frictionless, vertical guide of equation y = f(x) under the gravity force.

he tangential acceleration can be found with this equation (I'll skip how I got it):

I do not believe that the acceleration does not depend on f''

 

[Ovolollo]

The equation of motion can be obtained by differentiating of the energy integral in time:
$$\frac{m}{2}|v|^2+mgf(x)=h,\quad |v|^2=\dot x^2+(f'(x)\dot x)^2.$$
There are a lot of standard tools for ode solving as well. Maple for example.

I do not believe that the acceleration does not depend on f''

Thank you very much wrobel for your answer. I really like your suggestion to use an energy approach. I'm really glad you suggest this formula. I never thought to write velocity like you did, and it was under my eyes for so long.
$$|v|^2=\dot x^2+(f'(x)\dot x)^2$$

Regarding the acceleration, I underline that this expression is the tangential acceleration (even if I used the letter a, that, I understand, is actually misleading).

Here how I found it:
The black continuous line is the curve, the gray vector is g and the blue angle is beta. Alpha is the purple angle.

So what I called a, is actually just the tangential component responsible for speed variation in magnitude (not direction).

 

[wrobel]

it is not an equation of motion yet. Now you need to obtain the acceleration from kinematics to have $\ddot x=f(x,\dot x)$