- #1
andyrk
- 658
- 5
Why is there no component of tangential acceleration in uniform circular motion? I think its because when we apply the WE Theorem (Work-Energy Theorem) as follows:
Work Done = ΔKE
=> F.S = 1/2*m*(vf2 - vi2),
=>(ma).s = 1/2*m*(vf2 - vi2)
=> (ma).s = 1/2*m*(0) (since the speed remains constant in uniform circular motion)
=> mascosθ = 0
=> θ = 90°
That means the angle between a and s is 90°. So in this case the acceleration of the particle is purely centripetal. This can also be seen by the fact that when we compute Δv over a very small time interval Δt, the resulting vector (that we would get from calculating the difference of vectors Δv) would always point towards the centre or in other words, it would be centripetal acceleration. So that's why there is no tangential component in uniform circular motion.
But how does this component change the direction of the particle so as to keep the velocity tangential at all points? Can someone show it quantitatively using equation in vector form?
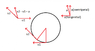
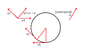
Coming to non-uniform circular motion, the a we get from computing Δv over a very small time interval Δt points as shown in the attachment. We break this a into 2 components, one of which comes out to be centripetal and the other one comes out to be tangential. As I discussed above, the centripetal component cannot increase the velocity, so it has to be the tangential one that does that.
My question is, firstly how does the combination of centripetal and tangential acceleration work in this case so as to keep the particle moving along the tangent at all points as well as increase its velocity, simultaneously? Can anyone show it quantitatively by using equations of motion in vector form?
Secondly, when we decompose the acceleration into two components, its upon us as to how we decompose them , meaning that the choice of axis is ours. So usually we take the normal x and y axis, so that y points towards the centre and x would hence automatically point tangentially. But what if we don't do it that way? Then the components we would get would be different and we won't be able to generalize that one of the components cannot increase the speed. It would be very confusing that way.
Work Done = ΔKE
=> F.S = 1/2*m*(vf2 - vi2),
=>(ma).s = 1/2*m*(vf2 - vi2)
=> (ma).s = 1/2*m*(0) (since the speed remains constant in uniform circular motion)
=> mascosθ = 0
=> θ = 90°
That means the angle between a and s is 90°. So in this case the acceleration of the particle is purely centripetal. This can also be seen by the fact that when we compute Δv over a very small time interval Δt, the resulting vector (that we would get from calculating the difference of vectors Δv) would always point towards the centre or in other words, it would be centripetal acceleration. So that's why there is no tangential component in uniform circular motion.
But how does this component change the direction of the particle so as to keep the velocity tangential at all points? Can someone show it quantitatively using equation in vector form?
Coming to non-uniform circular motion, the a we get from computing Δv over a very small time interval Δt points as shown in the attachment. We break this a into 2 components, one of which comes out to be centripetal and the other one comes out to be tangential. As I discussed above, the centripetal component cannot increase the velocity, so it has to be the tangential one that does that.
My question is, firstly how does the combination of centripetal and tangential acceleration work in this case so as to keep the particle moving along the tangent at all points as well as increase its velocity, simultaneously? Can anyone show it quantitatively by using equations of motion in vector form?
Secondly, when we decompose the acceleration into two components, its upon us as to how we decompose them , meaning that the choice of axis is ours. So usually we take the normal x and y axis, so that y points towards the centre and x would hence automatically point tangentially. But what if we don't do it that way? Then the components we would get would be different and we won't be able to generalize that one of the components cannot increase the speed. It would be very confusing that way.