Equation of Motion of a System of Springs (System Dynamics)

[LostMechE901]

I'm having trouble understanding the forces involved when defining the equation of motion for this particular problem.

So... I've seen the answer for the eq. of motion worked two different ways. The first way involves combining the spring series into K_eq = K₁⋅K₂/(K₁+K₂). The answer, plugging in α(K₁) for K₂, comes out to be M×x" + α(K₁)/(1+α) × (x + δ_st) = mg. The weight and static deflection cancel out, rendering the final answer M×x" + (x) × (α(K₁)/(1+α)) = 0.

The 2_nd way I've seen this problem worked is as follows:

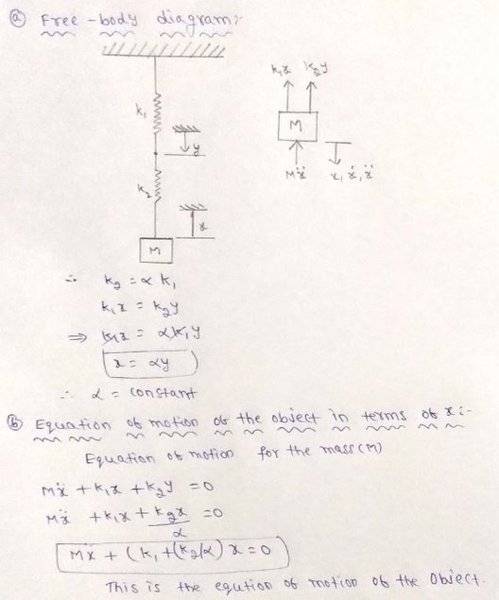
In the 2nd solution, I don't understand how he figured the proportion K₁⋅x = K₂⋅y. When drawing my free body diagrams of the springs enacting forces upon each other, the only equations I can devise are K₂(y-x) ∧ and K₁⋅y ∧.

Is the 2nd solution incorrect? If it can be worked that way, how do you figure that relationship?

*Edit* I Just realized there is a specific engineering problem help section for threads like this. I apologize for misplacement in advance.

 

[Chestermiller]

The 2nd solution is incorrect. The equation should read: $$K_2(x-y)=K_1x$$ This leads to the same result as in the first solution.