Equations of two concentric paraboloids

[MCB277]

Homework Statement

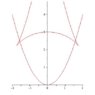
I need to obtain the equation of 2 paraboloids separated by a distance L.

Homework Equations

I think that the equations should be:

z_1=x^2+y^2
z_2=x^2+y^2-L

The Attempt at a Solution

The problem is that when I plot the region between two inequations,
x^2+y^2>=z and z+L>=x^2+y^2
the region is not of size L

Thanks[/B]

 

[Orodruin]

What you have done is to construct two paraboloids that are separated by a distance $L$ in the $z$-direction. Being separated by $L$ in the $z$-direction is not the same thing as the closest point on the second surface to a given point on the first being a distance $L$ away. In order to solve the problem, you need to specify which of these is your intended problem and solve that problem.

Edit: It should also be pointed out that the curve that is everywhere a distance $L$ away from a paraboloid is not a paraboloid in itself.

 

[MCB277]

So, if I want to build a paraboloid with a certain thickness L, how would it be done?

 

[Orodruin]

So, if I want to build a paraboloid with a certain thickness L, how would it be done?

You cannot. A paraboloid is a hypersurface of one dimension lower than the space you are constructing it in. It does not have a thickness.

 

[MCB277]

you are right there is no such thing, I want to find a surface parallel to the paraboloid given in that equation.

 

[Orodruin]

So for a given point on the paraboloid, what is the normal vector to the paraboloid?

 

[MCB277]

Thanks you !

 

[RPinPA]

Thanks you !

Do you think you could follow up here or via message how you proceeded from this point?

I made an attempt to do the analogous problem in one variable, starting with y = x^2 and its normal vectors, but I got buried in algebra trying to convert the resulting equations for "the point (x1, y1) which is distance L from (x, x^2) along the normal" to a closed form y1 = f(x1).

 

[LCKurtz]

Do you think you could follow up here or via message how you proceeded from this point?

I made an attempt to do the analogous problem in one variable, starting with y = x^2 and its normal vectors, but I got buried in algebra trying to convert the resulting equations for "the point (x1, y1) which is distance L from (x, x^2) along the normal" to a closed form y1 = f(x1).

Since this isn't the OP's question, I will give a bit more suggestion to you. Let's write the parabola in vector form $\vec r(t) = \langle t, t^2\rangle$. A tangent vector is $r'(t) = \langle 1,2t \rangle$ and a unit normal pointed down is $\hat n(t) =\frac 1 {\sqrt{1+4t^2}}\langle 2t,-1\rangle$. Now let's say you want a parallel curve $h$ distance from and below the parabola, use$$
\vec q(t) = \vec r(t) +h\hat n(t)$$Here's a picture with $h=1$:

 

[RPinPA]

Pretty much what I did, giving me $<q_1(x), q_2(x)>$ parametrically in terms of $x$. But I was hoping to eliminate the $x$ so that I could analyze the result to describe exactly what kind of curve it is, if not a parabola.

 

[LCKurtz]

Pretty much what I did, giving me $<q_1(x), q_2(x)>$ parametrically in terms of $x$. But I was hoping to eliminate the $x$ so that I could analyze the result to describe exactly what kind of curve it is, if not a parabola.

I don't think you will have much luck with that in general. For example, if you take the parabola $y = x^2$ and look for the curve that three units away and parallel "above" it, that is too high to fit above it near the vertex and you get a graph that looks like this:

The equation for that is$$
\vec R(t) =\langle t - \frac{6t}{\sqrt{1+4t^2}}, t^2 - \frac{3}{\sqrt{1+4t^2}} \rangle$$I haven't tried it, but looking at the image I'm guessing if you manage to put this in the $y = f(x)$ form, it won't be either simple or and some "standard" form you would recognize. It gets even more interesting if you do the same thing to an ellipse and put the second curve too far on the inside.