I Error Propagation in Transcendental Equation

[jst6981]

Hey guys,

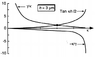
I'm in a class where we're learning about waveguides, and without going into too much depth, we often solve an equation

$$ \tan{(\kappa (\frac{a}{2}))} = \frac{\gamma}{\kappa} $$

for $\kappa$ numerically since there isn't an analytic solution for $\kappa$. I'm doing a project where $a$ has an error $\Delta a$, and I want to be able to solve this in a way so that I have a $\kappa$ written $\kappa \pm \Delta \kappa$ so that I can propagate the error in $\kappa$ due to the error in $a$ throughout the rest of my calculations for the project.

If anybody has a nice way I can do this, please let me know. I appreciate help in advance!

 

[mfb]

Vary a by Δa up and down, solve for $\kappa$ in both cases. If the resulting deviations of $\kappa$ are reasonably symmetric, use that as uncertainty. Otherwise it might need more sophisticated approaches.

 

[jst6981]

I had considered that, each function is roughly linear when they intersect as below.

I think it may work

 

[haruspex]

If you write that k is a function of a and differentiate your equation wrt a, you can eliminate the trig and get a differential equation for k. Manipulate that to get k' as a function of k and a.

 

[ChrisVer]

Do you want an analytical solution or you are fine with using numerical solutions?
In the latter you can generate some toys, let's say 10,000...
In each toy, you randomly sample \alpha from a gaussian (for example) with mean \alpha and standard deviation \Delta \alpha, so that you get a set \{\alpha_i\} , i=1,~2,~...,~10000 measurements...
You can get the \{k_i\} set from your equation.
See how it's distributed and try to find the 68% central coverage (aka determine \Delta k_{\pm} where plus/minus means the up/down uncertainty - that means the range [nominal-down, nominal] contains the 34% of your toys and the range [nominal,nominal+up] contains the other 34%)...