Forcefedglas
- 26
- 0
Homework Statement
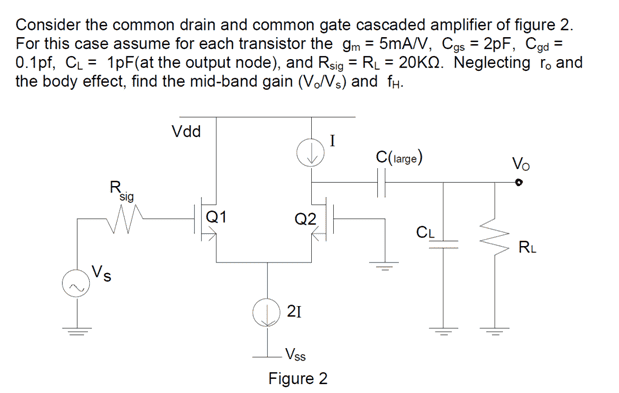
I've found the gain, but now I need to estimate the upper cutoff frequency with the open circuit time constant method, so the upper 3dB cutoff would roughly be $$\sum_{i = 1}^{n} \frac{1}{\tau_i}$$
The attempt at a solution
I'm currently trying to make sense of the given solutions:
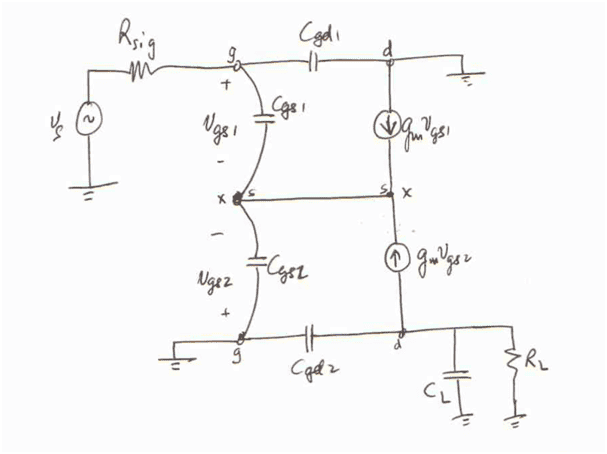
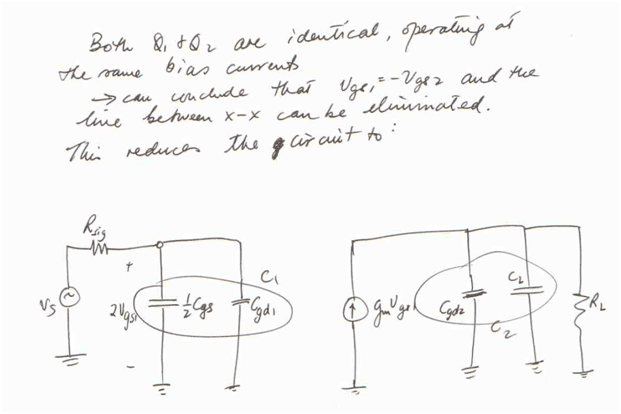
I got something similar to the first picture after drawing out the small signal equivalent, but I'm completely lost as to how they went from that circuit to the one in the second picture. Why does the drain of Q2 suddenly become grounded, and how did the GS capacitors combine and turn into half of their original value? I've tried searching around but haven't found any explanations of the simplification method used here.
I attempted to use a 1v test voltage at the gate source capacitors (in the first circuit) to find the equivalent resistance seen by them but that yielded a different answer to what I get if I work it out via the second circuit.
Any help/tips would be greatly appreciated, thanks.
I've found the gain, but now I need to estimate the upper cutoff frequency with the open circuit time constant method, so the upper 3dB cutoff would roughly be $$\sum_{i = 1}^{n} \frac{1}{\tau_i}$$
The attempt at a solution
I'm currently trying to make sense of the given solutions:
I got something similar to the first picture after drawing out the small signal equivalent, but I'm completely lost as to how they went from that circuit to the one in the second picture. Why does the drain of Q2 suddenly become grounded, and how did the GS capacitors combine and turn into half of their original value? I've tried searching around but haven't found any explanations of the simplification method used here.
I attempted to use a 1v test voltage at the gate source capacitors (in the first circuit) to find the equivalent resistance seen by them but that yielded a different answer to what I get if I work it out via the second circuit.
Any help/tips would be greatly appreciated, thanks.