Euler Lagrange equation and a varying Lagrangian

[Tamin Ayoub]

Homework Statement

The variation of the Lagrangian with respect to PSI and X

Relevant Equations

Euler Lagrange equation

Hello, I have been working on the three-dimensional topological massive gravity (I'm new to this field) and I already faced the first problem concerning the mathematics, after deriving the lagrangian from the action I had a problem in variating it
Here is the Lagrangian

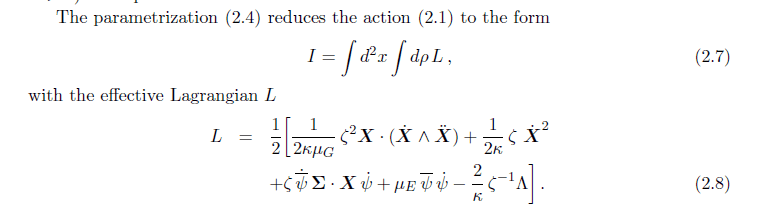
The first variation should be with respect to Ψ I tried to find this result

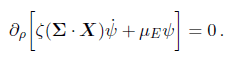
but I had a sign different, my result had a Minus sign.

The second variation is with respect to the vector X, note that

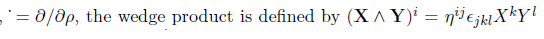
and the result is

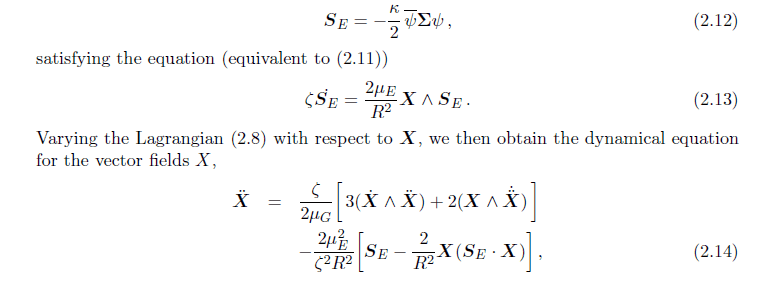
I tried to use the euler lagrange equation to find this result but i don't have much experience dealing with this wedge product variation

thank you in advanced

 

[Nate810]

for helping me The Euler-Lagrange equation for the variation with respect to $\Psi$ is given by\begin{align}\frac{\delta L}{\delta \Psi} = \frac{\partial L}{\partial \Psi} - \nabla_\mu \frac{\partial L}{\partial (\nabla_\mu \Psi)} = 0.\end{align}A few notes:1) The second term on the right-hand side, $\nabla_\mu \frac{\partial L}{\partial (\nabla_\mu \Psi)}$, involves taking the partial derivative of the Lagrangian with respect to the covariant derivative of $\Psi$. This is done using the Leibniz rule.2) The wedge product of two vectors, $X$ and $Y$, is defined as\begin{align}X \wedge Y = \frac{1}{2!} (X \cdot \nabla) Y - \frac{1}{2!} (Y \cdot \nabla) X.\end{align}Using this definition, we can rewrite the second variation in terms of derivatives of the Lagrangian with respect to $X$ and $Y$:\begin{align}\frac{\delta^2 L}{\delta X \delta Y} &= \frac{\partial^2 L}{\partial X \partial Y} - \frac{1}{2!}\left(\frac{\partial L}{\partial (\nabla_\mu X)} \cdot \nabla_\mu \right) Y - \frac{1}{2!}\left(\frac{\partial L}{\partial (\nabla_\mu Y)} \cdot \nabla_\mu \right) X \\&+ \frac{1}{4!}\left(\frac{\partial L}{\partial (\nabla_\mu \nabla_\nu X)} \cdot \nabla_\mu \nabla_\nu \right) Y - \frac{1}{4!}\left(\frac{\partial L}{\partial (\nabla_\mu