zak100
- 462
- 11
Homework Statement
I think I am evaluating a wrong value for eigen vector. Wrong in the sense that first row is giving different value and next row is giving a different value.
The matrix is:
[0 1]
[-2 -3]
My eigen values are λ=-1 & λ=-2. I get the fine vectors for λ=-1 but λ=-2 x vanishes.
Homework Equations
A-λI = 0
& Ax = λx
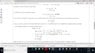
The Attempt at a Solution
[0 1] * [x] = -2 * [x]
[-2 -3] [y] [y]
First row gives: y = -2x -2y
2x = 3y
Now x = 2/3 y
μ =[2, 3] (instead of column, i am showing row vector)
But the second row gives me: -2x -3y = -2x -2y (therfore x vanishes)
they have evaluated
μ=[1, -2] (instead of column, i am showing row vector)
Some body please guide me.
Zulfi.
Attachments
Last edited: