dykuma
- 55
- 6
- Homework Statement
- I've been messing with this integral for a few days now, and have made no progress on it. I know what the the answer will be thanks to mathermatica, but I want to know how to do it myself.
- Relevant Equations
- N/A
the integral is:
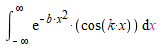
and according to mathematica, it should evaluate to be:
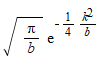 .
.
So it looks like some sort of Gaussian integral, but I'm not sure how to get there. I tried turning the cos function into an exponential as well:
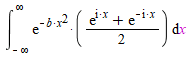
however, I don't think this helps the issue much.
and according to mathematica, it should evaluate to be:
So it looks like some sort of Gaussian integral, but I'm not sure how to get there. I tried turning the cos function into an exponential as well:
however, I don't think this helps the issue much.