Evaluating $M+N$ Given Triangle Congruency and Side Lengths

[anemone]

View attachment 1354

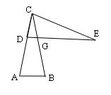
Given that triangle $ABC$ is congruent to triangle $CDE$, and that $\angle A=\angle B=80^{\circ}$. Suppose that $AC=1$ and \(\displaystyle DG=\frac{2\sin 10^{\circ}}{M+N\sin^2 10^{\circ}}\).

Evaluate $M+N$.
.

 

[MarkFL]

Re: Evaluate M+N

My solution:

Spoiler

We find that:

\(\displaystyle \angle C=180^{\circ}-2\cdot80^{\circ}=20^{\circ}\)

The Law of Cosines gives us:

\(\displaystyle \overline{CD}^2=2\left(1-\cos\left(20^{\circ} \right) \right)\)

Triangle $CDG$ is similar to the two congruent triangles, hence, we may state:

\(\displaystyle \frac{\overline{CD}}{\overline{DG}}= \frac{1}{\overline{CD}}\implies\overline{DG}= \overline{CD}^2= 2\left(1-\cos\left(20^{\circ} \right) \right)\)

Using a double angle identity for cosine, we may write:

\(\displaystyle \overline{DG}=2\left(1-\left(1-2\sin^2\left(10^{\circ} \right) \right) \right)=4\sin^2\left(10^{\circ} \right)\)

Thus, we see that we require:

\(\displaystyle M+N\sin^2\left(10^{\circ} \right)=\frac{1}{2}\csc^3\left(10^{\circ} \right)\)

With $M=0$, we then have \(\displaystyle M+N=\frac{1}{2}\csc^3\left(10^{\circ} \right)\)

 

[Opalg]

Re: Evaluate M+N

[sp]I agree with Mark as far as the line $DG = 4\sin^210^\circ$. But I wanted to express that in the form \(\displaystyle DG=\frac{2\sin 10^{\circ}}{M+N\sin^2 10^{\circ}}\), with $M$ and $N$ numerical constants (not involving $\sin10^\circ$). So I want to find $M$ and $N$ such that \(\displaystyle 4\sin^210^\circ = \frac{2\sin 10^{\circ}}{M+N\sin^2 10^{\circ}}\), or $2M\sin10^\circ + 2N\sin^310^\circ = 1$.

Remembering that $\sin3\theta = 3\sin\theta - 4\sin^3\theta$ and that $\sin30^\circ = 1/2$, I put $\theta = 10^\circ$, to get $\frac12 = 3\sin10^\circ - 4\sin^310^\circ$. Thus $6\sin10^\circ - 8\sin^310^\circ = 1$. Comparing that with the equation in the previous paragraph, you see that we can take $M=3$, $N=-4$ and hence $M+N = -1$.[/sp]

 

[anemone]

Re: Evaluate M+N

My solution:

Spoiler

We find that:

\(\displaystyle \angle C=180^{\circ}-2\cdot80^{\circ}=20^{\circ}\)

The Law of Cosines gives us:

\(\displaystyle \overline{CD}^2=2\left(1-\cos\left(20^{\circ} \right) \right)\)

Triangle $CDG$ is similar to the two congruent triangles, hence, we may state:

\(\displaystyle \frac{\overline{CD}}{\overline{DG}}= \frac{1}{\overline{CD}}\implies\overline{DG}= \overline{CD}^2= 2\left(1-\cos\left(20^{\circ} \right) \right)\)

Using a double angle identity for cosine, we may write:

\(\displaystyle \overline{DG}=2\left(1-\left(1-2\sin^2\left(10^{\circ} \right) \right) \right)=4\sin^2\left(10^{\circ} \right)\)

Thus, we see that we require:

\(\displaystyle M+N\sin^2\left(10^{\circ} \right)=\frac{1}{2}\csc^3\left(10^{\circ} \right)\)

With $M=0$, we then have \(\displaystyle M+N=\frac{1}{2}\csc^3\left(10^{\circ} \right)\)

Hi MarkFL,

Thanks for participating and since the problem doesn't mention any restriction on the variables $M$ and $N$, you got the full credit for your solution! Bravo!

But even though I am not the question setter, I should have noticed when I solved the problem that I should add the condition on both variables so that their sum is unique. I admit I overlooked this. I'm sorry...

[sp]I agree with Mark as far as the line $DG = 4\sin^210^\circ$. But I wanted to express that in the form \(\displaystyle DG=\frac{2\sin 10^{\circ}}{M+N\sin^2 10^{\circ}}\), with $M$ and $N$ numerical constants (not involving $\sin10^\circ$). So I want to find $M$ and $N$ such that \(\displaystyle 4\sin^210^\circ = \frac{2\sin 10^{\circ}}{M+N\sin^2 10^{\circ}}\), or $2M\sin10^\circ + 2N\sin^310^\circ = 1$.

Remembering that $\sin3\theta = 3\sin\theta - 4\sin^3\theta$ and that $\sin30^\circ = 1/2$, I put $\theta = 10^\circ$, to get $\frac12 = 3\sin10^\circ - 4\sin^310^\circ$. Thus $6\sin10^\circ - 8\sin^310^\circ = 1$. Comparing that with the equation in the previous paragraph, you see that we can take $M=3$, $N=-4$ and hence $M+N = -1$.[/sp]

Hi Opalg,

Thanks for participating and I must tell you when I arrived at the step where I got $2Q\sin^3 10^{\circ}+2P \sin 10^{\circ}-1=0$, I immediately thought of the triple angle formula for the function of sine and you're recent help to me in one of the simultaneous equation threads was the inspiration to me...so, I wouldn't have solved this problem if not for what you have taught me! (Sun)

 

[CellCoree]

I would first like to clarify that the given information is not sufficient to evaluate $M+N$. In order to find the value of $M+N$, we need to have more information about the triangles $ABC$ and $CDE$, such as their side lengths or angles.

However, based on the given information, we can make some observations. Since triangle $ABC$ is congruent to triangle $CDE$, we can conclude that $AB=CD$ and $BC=DE$. Also, since $\angle A=\angle B=80^{\circ}$, we can infer that $\angle C=\angle D=100^{\circ}$, as all angles in a triangle must add up to $180^{\circ}$.

Using the Law of Sines, we can write the following equations:

$\frac{AC}{\sin \angle C}=\frac{BC}{\sin \angle B}$ and $\frac{DG}{\sin \angle D}=\frac{CG}{\sin \angle C}$

Substituting the known values, we get:

$\frac{1}{\sin 100^{\circ}}=\frac{BC}{\sin 80^{\circ}}$ and $\frac{\frac{2\sin 10^{\circ}}{M+N\sin^2 10^{\circ}}}{\sin 100^{\circ}}=\frac{CG}{\sin 100^{\circ}}$

Simplifying these equations, we get:

$BC=\frac{\sin 80^{\circ}}{\sin 100^{\circ}}$ and $CG=\frac{2\sin 10^{\circ}}{M+N\sin^2 10^{\circ}}$

Again, we cannot solve for $M+N$ without more information. However, we can make some observations about the value of $M+N$ based on the given equation for $DG$. We can see that $M+N$ must be a positive value, as $\sin^2 10^{\circ}$ is always positive and $DG$ is given to be a positive value. Additionally, as $\sin 10^{\circ}$ is a small value, $M+N$ must be a large value in order for the fraction to be small.

In conclusion, based on the given information, we cannot evaluate $M+N$ accurately. We would need more information about the