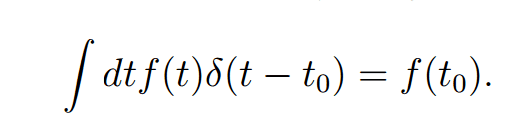SUMMARY
The forum discussion centers on evaluating a scattering integral involving the Dirac delta function and the vector element dk'. Participants emphasize the necessity of converting to spherical coordinates, where the Dirac delta function influences the integral over the radial component, r. Key points include the clarification that dk' represents an infinitesimal vector element rather than a derivative, and the importance of using the cosine law to express the distance between vectors in terms of k, k', and the angle θ. The discussion highlights the confusion surrounding the integration process and the role of the Dirac delta function in the evaluation of the integral.
PREREQUISITES
- Understanding of Dirac delta functions in integrals
- Familiarity with spherical coordinates in calculus
- Knowledge of vector calculus and infinitesimal elements
- Proficiency in using the cosine law for vector relationships
NEXT STEPS
- Study the application of Dirac delta functions in quantum mechanics
- Learn about spherical coordinate transformations in integrals
- Explore vector calculus, focusing on infinitesimal vector elements
- Investigate the cosine law and its applications in physics problems
USEFUL FOR
Students and researchers in physics, particularly those dealing with scattering theory, integrals involving Dirac delta functions, and vector calculus applications.
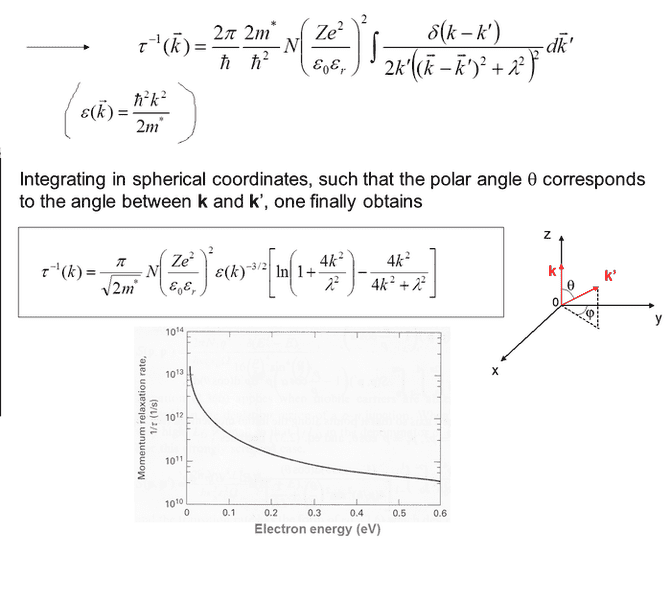 I tried something like the dirac function identity:
I tried something like the dirac function identity: