SUMMARY
This discussion focuses on evaluating surface integrals in the context of Gauss's Law, specifically for a tenth grader new to Advanced Calculus. The key takeaway is that a surface integral can be approached as nested ordinary integrals, allowing for integration over two variables, x and y. The process involves integrating one variable while treating the other as a constant, which can be done in either order. This foundational understanding is crucial for tackling problems related to surface integrals effectively.
PREREQUISITES
- Understanding of basic calculus concepts, including integration.
- Familiarity with Gauss's Law and its applications in physics.
- Knowledge of functions of two variables, specifically f(x,y).
- Experience with double integrals and their geometric interpretations.
NEXT STEPS
- Study the concept of double integrals in calculus.
- Learn about the applications of Gauss's Law in electromagnetism.
- Explore the geometric interpretation of surface integrals.
- Practice solving problems involving surface integrals in the x-y plane.
USEFUL FOR
This discussion is beneficial for high school students studying Advanced Calculus, particularly those interested in physics applications of calculus, as well as educators looking for ways to explain surface integrals and Gauss's Law.
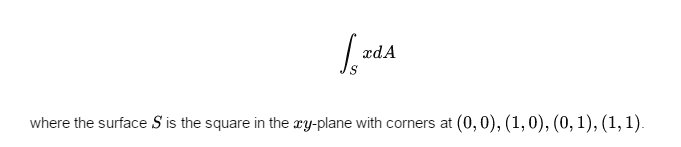 I couldn't attempt anything, having no knowledge over surface integration. So please help.
I couldn't attempt anything, having no knowledge over surface integration. So please help.