Excel projectile trajectory

[swemek]

Hello!

I'm doing some research for a small project that I hope you can help me with. I'm not a math genius, I just have an idea.

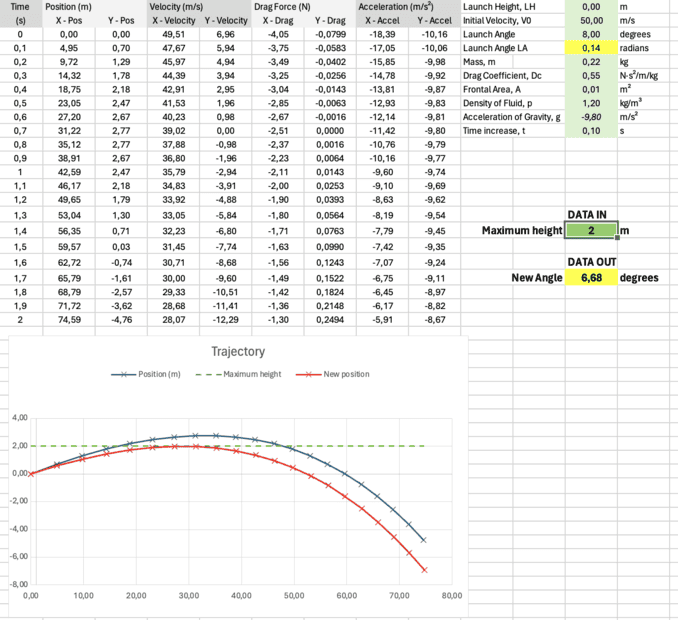
I have an Excel document of a projectile trajectory with an angle of 8 degrees. (Can be any angle.) Blue projectile trajectory.

What I want to do is enter the maximum height (green dashed line) and get a new angle. Red projectile trajectory. Calculated on a different tab.
I only tried my way up to the angle of 6.68 degrees.

Formulas used in Excel:
X-pos =B3+D3*t
Y-pos =C3+E3*t
X-Velocity =V0*COS(LA) =D3+H3*t
Y-Velocity =V0*SIN(LA) =E3+I3*t
X-Drag =-1/2*Dc*A*p*D3^2
Y-Drag =-1/2*Dc*A*p*E3^2
X-Accel =F3/m
Y-Accel =(G3+m*g)/m

Is this doable?

Hope you can help me.
Thanks in advance /M

 

[A.T.]

X-Drag =-1/2*Dc*A*p*D3^2
Y-Drag =-1/2*Dc*A*p*E3^2

This won't work. Since drag is non-linear, you cannot split its calculation into X & Y components like that. You have to compute the total XY-speed, use that for total XY-drag, and split that in X & Y drag components.

As for your main question. You probably need something like this:
https://www.tutorialspoint.com/exce...a_analysis_optimization_with_excel_solver.htm
Decision Variable Cell : launch angle
Objective Cell (to be minimized) : (MAX(Y_POS) - TARGET_MAX_Y_POS)^2

 

[pbuk]

Objective Cell (to be minimized) : (MAX(Y_POS) - TARGET_MAX_Y_POS)^2

Is your recommendation of this rather than simply MAX(Y_POS) - TARGET_MAX_Y_POS based on experience?

 

[Ibix]

Is your recommendation of this rather than simply MAX(Y_POS) - TARGET_MAX_Y_POS based on experience?

If you minimise the difference I would expect the optimizer to aim for max(y_pos) tending to negative infinity, since that minimises the value. If you minimise the squared difference the optimiser should aim for equality.

 

[A.T.]

Is your recommendation of this rather than simply MAX(Y_POS) - TARGET_MAX_Y_POS based on experience?

This won't work for the reason stated by @Ibix. One could try ABS(MAX(Y_POS) - TARGET_MAX_Y_POS), but squaring the difference is usually more numerically stable, because of the smooth 1st derivative.

 

[pbuk]

This won't work for the reason stated by @Ibix. One could try ABS(MAX(Y_POS) - TARGET_MAX_Y_POS), but squaring the difference is usually more numerically stable, because of the smooth 1st derivative.

Ah sorry, I should have been clearer.

In solving similar problems I have always solved for a difference of zero by using Data -> What-If Analysis -> Goal Seek.

I do this because I have always done it this way and I wondered if you had experience that showed any option within the Analysis Tool Pack was faster/more stable/more accurate precise.

In any case for the problem in the OP, using Goal Seek would be perfectly adequate.

 

[A.T.]

In any case for the problem in the OP, using Goal Seek would be perfectly adequate.

@swemek Yes, since you have only one parameter you can use Goal Seek as well:
https://www.tutorialspoint.com/excel_data_analysis/what_if_analysis_with_goal_seek.htm