JacobS. said:
where does the actual force holding them together come from? Is it simply the fact that there is a constant equilibrium and exchange of particles?
Cause and effect in quantum physics can be a little problematic to find. The way these theories were first defined by Feynman was to make a list of all the elementary things that can happen - like "a particle moves from A to B" and "at a point in space, particle X turns into particles Y and Z" - and then each basic possibility has a "probability amplitude" (which is a complex number that you square to get a probability). And then, if you want the probability for something to happen, like "proton and neutron exchange a pion", you have to consider all the ways that you can build that complex process out of the elementary processes, and apply the probability rules to get your answer.
So let's consider the simpler case of a hydrogen atom - a proton and an electron held together by electromagnetism. In classical physics you say: the proton and the electron each have a charge, and they each produce a little electric field. And the charge of a particle both determines how strong its field is, and also determines how the particle moves in response to the field of another particle. In quantum physics you say that electromagnetism consists of photons, and the force field is just a shorthand for photon probabilities, and the charge of a particle tells you the probability that it emits or absorbs a photon. So when you want to understand why the proton and the electron stick together, not in terms of force fields, but in terms of photons, it ends up being a statement about how the quantum probabilities for particle motion and particle interaction add up to produce a most-probable behavior (i.e. the atom stays in one piece).
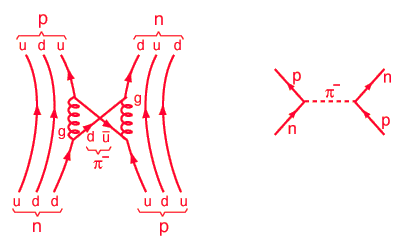
It's like this for why the quarks inside a proton, or inside a pion, stick together. You can think in terms of a "chromoelectric field" or color force field that each quark emits, but once again, that's just a shorthand for gluon probabilities. And the way the probabilities come together for quarks and gluons is a lot more complicated than for photons, because gluons themselves can emit gluons, because color charge is more complicated than electric charge (red, blue, green, not just positive and negative), and also because the probability to emit gluons is very high. The classical-physics prototype for why the atom holds together is just circular motion, like a planet orbiting a star, but then with some extra complications because of how quantum probabilities work (e.g. the possible "orbits" of an electron come in discrete levels). With quarks, the intuitive pictures are more complicated and also somewhat disputed. In some sense, a pion is probably a "flux tube" of gluons going back and forth between the quark and the antiquark, and a proton or neutron may be a "bag" in which the three quarks are surrounded by a whole cloud of gluons and transiently existing quarks and antiquarks. (These "pictures" are simple mathematical approximations that people use in order to calculate, they're not just words.)
Since you mention that gluons have no component parts, I should clarify something else about these basic interactions. I mentioned that, the way Feynman did it, the definition of the theory, its starting point, is to say, there are two sorts of things that can happen, a particle moves, and a particle is replaced at the same point by some other particles, and then we have rules of calculation for probabilities. If you took that description absolutely seriously, then what happens when you have quark-antiquark creation from a gluon, is that the gluon simply ceases to exist and is immediately replaced with a quark and an antiquark at the same point in space where the gluon was.
If you went to a deeper framework, like string theory, the theory might tell you more. In string theory, such an event would correspond to a gluon string splitting into a quark string and an antiquark string. Also, mathematics usually offers many different ways of looking at something, and it's fairly certain that there are other, quite different ways of organizing and interpreting the calculations that give you the probabilities. The "twistor" approach to field theory is causing a slow mathematical revolution at the moment, which I am sure will ultimately result in new physical concepts, but I don't know what they are at this point.
But if we just stick with the picture that physicists still learn in university, the picture of particles interacting according to the rules of quantum probability, then it's as I have described it.