Quarky nerd
- 10
- 0
fig 1
Given:
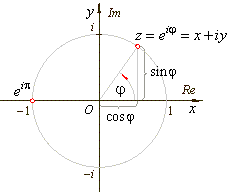
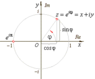
eiΘ= cosΘ + i sinΘ (radians)
eπi=-1
Deduced
e2πi=(-1)2
e2πi=1
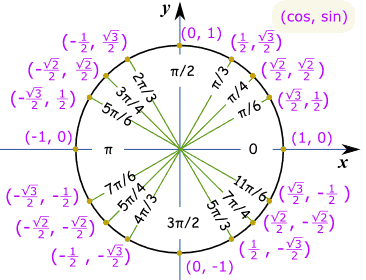
e(2/3)πi=11/3
e(2/3)iπ=1
e(2/3)iπ=cos(2i/3)+i sin(2i/3)
e(2/3)iπ=-1/2+i(3/2)
-1/2+i(31/2/2)=1
where n is greater than or equal to 1 or n=a/b where a is greater than or equal to 1 and b is odd
1n=1
∴
(-1/2+i(3/2))n=1However this is absurd and I
have no idea what's wrong
(sorry about the formating it was better in docs)
Given:
eiΘ= cosΘ + i sinΘ (radians)
eπi=-1
Deduced
e2πi=(-1)2
e2πi=1
e(2/3)πi=11/3
e(2/3)iπ=1
e(2/3)iπ=cos(2i/3)+i sin(2i/3)
e(2/3)iπ=-1/2+i(3/2)
-1/2+i(31/2/2)=1
where n is greater than or equal to 1 or n=a/b where a is greater than or equal to 1 and b is odd
1n=1
∴
(-1/2+i(3/2))n=1However this is absurd and I
have no idea what's wrong
(sorry about the formating it was better in docs)
Attachments
Last edited: