- #1
Est120
- 54
- 3
- Homework Statement
- find the appropiate Navier-Stokes equation in the low Re number limit
- Relevant Equations
- Navier Stokes equations
in the limit as Re→0 , we can neglect the material derivate of v ( Dv/Dt =0 ) but why in books they always make the gravity effects equal to 0?
i can't understand and no one really explains this stuff
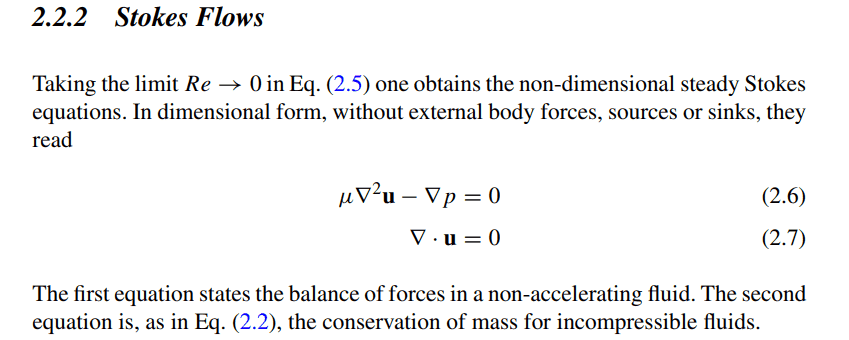
i can't understand and no one really explains this stuff