Extreme focus of a radially polarized beam

Click For Summary
SUMMARY

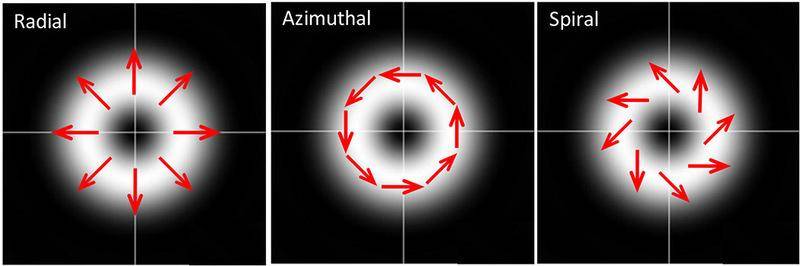
The discussion centers on the behavior of a radially polarized beam when focused to a single point. It concludes that while destructive interference may occur, diffraction limits the extent of focusing, resulting in a finite beam width and a characteristic diffraction pattern. The energy of the beam does not completely cancel out at the focus; instead, it produces a bright diffraction ring around the center. The phenomenon has been documented in the study titled "3-dimensional local field polarization vector mapping of a focused radially polarized beam using gold nanoparticle functionalized tips," published in OPTICS EXPRESS.

PREREQUISITES
  • Understanding of radially polarized beams
  • Knowledge of diffraction patterns and their implications
  • Familiarity with constructive and destructive interference
  • Basic principles of electromagnetic field vectors
NEXT STEPS
  • Research the principles of diffraction and its effects on beam focusing
  • Study the paper "3-dimensional local field polarization vector mapping of a focused radially polarized beam using gold nanoparticle functionalized tips"
  • Explore advanced optics techniques for manipulating polarized light
  • Investigate applications of radially polarized beams in nanotechnology and imaging
USEFUL FOR

Optical physicists, researchers in photonics, and engineers working with laser technologies will benefit from this discussion, particularly those focused on beam manipulation and polarization effects.

Pakano
Messages
3
Reaction score
0
What happen if a radially polarized beam is extremely focused to a single spot?
Is it disappeared because E-fields in opposite direction subtract each other?

004965_10_fig1.jpg
 
Science news on Phys.org
:welcome:
Are you asking about constructive / destructive interference?
 
anorlunda said:
:welcome:
Are you asking about constructive / destructive interference?
Yes, does destructive interference happen when focusing a radially polarized beam?
 
Could I re-word your idea a bit? You appear to be concerned that your image would appear to be focussed at a single point but that would involve the beam energy all being canceled out and it has to go somewhere so wtf?
Diffraction comes to your rescue. There is a limit to how small your 'single point' can be.
Addition of the field vectors depends on their direction and also on the exact point at which you are doing the calculation. The resultant of focussing all the parts of the beam will be the vector sum of all the elemental parts of the beam, at any point. But there is no single point where all the beam will focus; there is always a 'sinx/x' type pattern around the nominal focus point. If it's all symmetrical (for all three examples), I would expect to find a zero but, off axis, you will not get total cancellation and the energy would be diverted. However 'tight' you try to make the optics, there is always a finite beam width and the resulting image will have places where there is no cancellation
But the beam has a zero at its centre in any case, in your diagrams. Its image must also have zero value at the centre if it has circular symmetry. You will get a bright diffraction ring around the centre with a radius that's related to 1/d, where d is the aperture of your optics.
 
Thank you guys!
 

Similar threads

Graduate The coherence length is much longer than the manufacturer claims
  • · Replies 10 ·
Replies
10
Views
3K
Graduate Weird pattern for a laser beam spot
  • · Replies 9 ·
Replies
9
Views
3K
Graduate Laser light vs "Regular" Light
  • · Replies 14 ·
Replies
14
Views
3K
Graduate Intensity of a Gaussian laser beam
  • · Replies 5 ·
Replies
5
Views
4K
Undergrad Light Polarization Reflected from Parabolic Mirror
  • · Replies 15 ·
Replies
15
Views
8K
Undergrad How Does Light Remain After Polarization Despite Changes in Its Electric Field?
  • · Replies 10 ·
Replies
10
Views
3K
Graduate Simple math model for a Particle Image Velocimetry system
  • · Replies 6 ·
Replies
6
Views
951
Graduate Light beam propulsion without lasers?
  • · Replies 25 ·
Replies
25
Views
4K
Graduate How Can I Mathematically Represent the Polarization of a Laser Beam?
  • · Replies 1 ·
Replies
1
Views
6K
Graduate Imperfectly Phase-Modulated Light / Residual Amplitude Modulation
  • · Replies 2 ·
Replies
2
Views
1K