Faraday's law on rotating disk

[gralla55]

Homework Statement

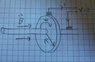
A metal disk is rotating with constant angular velocity in a constant magnetic field perpendicular to it. Use Faraday's law to fint the the induced voltage difference between the two points on the wire.


The attempt at a solution

So to use Faraday's Law, I need to first find an expression for the change in magnetic flux per unit of time inside a closed loop. However, from the drawing I can't find any loop where the magnetic field changes. The wire is connected to the disk with brushes, so I'm assuming that it doesn't rotate with the disk. Though, even if it did the magnetic field would still not penetrate it's interior.

 

[technician]

Look at the line marked R. It is sweeping out an area in the magnetic field.

 

[gralla55]

Sure, but the magnetic field is constant, so how is the flux through that area changing with time?

 

[technician]

Check Classical physics, page2 , post by HAMJOOP...faraday paradox.
There is a minor mistake in post #10 but I think this thread will help.

 

[rude man]

One way to handle this problem is to think of the disc as comprising many radial strips of copper separated by very thin insulating material. Now compute the emf generated by one of those strips.

Then realize that all the strips are connected in parallel so the emf is the same as if there were only one strip.

Now you have to justify the presence of the insulating strips. Hint: if there is no current from one point to another, is it OK to put an insulator between those points?