Fermat's principle seems indefinite

[Anton Alice]

Hello forum,

please take a look at the following picture:

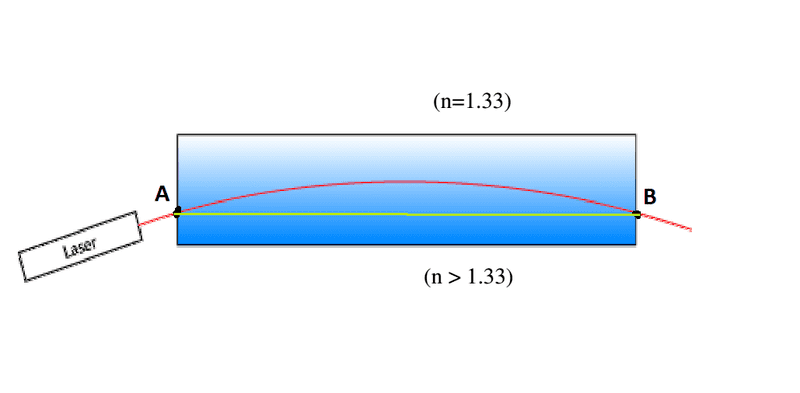It's a salt solution, with increasing refractive index, as you go down the solution.

How can I explain this with Fermat's principle?
Let's set the starting point A to the point, where the laser beam penetrates the left wall of the container.
The ending point B shall be the intersection of the laser beam with the right container wall. I suppose, that A and B are at same height.

Fermat says, that a path between a starting point A and an ending point B needs to be extremal in terms of optical pathlength.
Apparently the optical path length of the red arc in the picture is shorter than the linear green path from A to B, because the linear path is in a more refractive medium.
But I could also go from A to B on a linear path by pointing the laser perpendicular to the container wall, so that the beam travels along a constant index of refraction, and therefore experiencing no deviation from the linear path.

Seemingly Fermat's Principle doesn't give all possible solutions here. In fact, Fermat's principle would forbid the green path, because its not extremal in terms of path length.

 

[just dani ok]

AFAIK Fermat mention about the path which require minimum travel time, not merely straight line distance.

 

[A.T.]

But I could also go from A to B on a linear path by pointing the laser perpendicular to the container wall, so that the beam travels along a constant index of refraction, and therefore experiencing no deviation from the linear path.

If you have a vertical gradient in the whole container, then the beam will deviate from the horizontal, and won't reach B anymore.

If you have no vertical gradient at the elevation of A & B, just somewhat above them, then you have two local extrema, which both satisfy Fermat's principle:

https://en.wikipedia.org/wiki/Fermat's_principle

...a more modern statement of the principle is that rays of light traverse the path of stationary optical length with respect to variations of the path.[2] In other words, a ray of light prefers the path such that there are other paths, arbitrarily nearby on either side, along which the ray would take almost exactly the same time to traverse.

 

[Anton Alice]

I stated Fermats Principle correctly:

Fermat says, that a path between a starting point A and an ending point B needs to be extremal in terms of optical pathlength.

I just used a german speaking style. I called it "extremal", which has the same meaning like saying, the functional of path length is stationary at a certain path-function.

If you have a vertical gradient in the whole container, then the beam will deviate from the horizontal, and won't reach B anymore.

If you have no vertical gradient at the elevation of A & B, just somewhat above them, then you have two local extrema, which both satisfy Fermat's principle

Well, there is a vertical gradient. But if I take a horizontal path, which is perpendicular to the gradient, then the path should not experience a deviation, because Snells law say so: The path is going along a layer of constant index of refraction.
And the problem is, that Fermat would forbid this path, because this path is not a stationary point of the length-functional. Right? Why do I think that? Because there is a vertical gradient. For example: If I make a small upward deviation, such that the green path now becomes more like the red path, i.e. a lightly curved path, then the optical path should become a little shorter. If I curve down the green path slightly, then the optical length should become a little longer, because the index of refraction increases, as we go down the solution. Therefore, If the one deviation makes the path shorter, and the other makes it longer, then the green path cannot be a stationary point (unless it is a saddle point or something like that...)

 

[A.T.]

Well, there is a vertical gradient. But if I take a horizontal path, which is perpendicular to the gradient, then the path should not experience a deviation,

Wrong.

https://en.wikipedia.org/wiki/Gradient-index_optics

 

[Anton Alice]

Aha, ok. So if I have for example a water surface (n=1,3), and air above it(n=1), then if I point a laser beam exactly along the surface plane of the water-air transition, then the laser beam should be refracted into the water? How does it come to that?

I can only explain that, by inverting the direction of a beam, that is just totally internally reflected.
But normally, in case of total internal reflexion, the beam goes from inside the water to the transition zone, and gets completely reflected according to fresnel ( transmission = 0). So there is actually no beam refracted along the water surface. And I find it curious, to invert the direction of a beam, that does not exist.

 

[A.T.]

Aha, ok. So if I have for example a water surface (n=1,3), and air above it(n=1), then if I point a laser beam exactly along the surface plane of the water-air transition, then the laser beam should be refracted into the water? How does it come to that?

A water surface is a discontinuity, not a smooth gradient. You should try to understand how refraction follows from differential propagation speeds:

This should make obvious, what happens if the propagation speed has a gradient perpendicular to the beam direction. Also demonstrated here:

 

[Anton Alice]

Cool video. the Grass stripe acts like a waveguide.

Referring to the pictures of huygens principle:

It is now quite clear, why there is a refraction into the lower medium, if the incoming beam travels along the surface transition.
But shouldn't be there actually two refractions? one into the lower medium, and one into the upper medium?I think that, because the secondary spherical waves by huygens should propagate in both media.