- #1
EternusVia
- 93
- 10
Hi everyone,
I'm taking my second semester of calc based physics this coming spring. I have a question in optics stemming from my reading of Feynman's lectures on physics. He gives a rough definition of Fermat's principle of least time as follows:
"... out of all possible paths that it might take to get from one point to another, light takes the path which requires the shortest time." (Feynman's emphasis)
My question is this. We know that there exist certain refractive indices for light as it passes through various media. Say we have a rectangular prism. Light is hitting one of the long edges at an angle. According to my understanding of Fermat's PoLT as stated above, the light should travel through the prism forming a right angle at the entry point and a right angle at the exit point (on the inside of the prism). This would minimize the amount of time that the light is in the slow medium, the glass. The total travel time for light would also be minimized, I think.
Of course, this doesn't happen in real life. So my understanding of Fermat's PoLT must be lacking. Could someone explain where I'm going wrong with light and the principle of least time?
Something like this happens in real life:
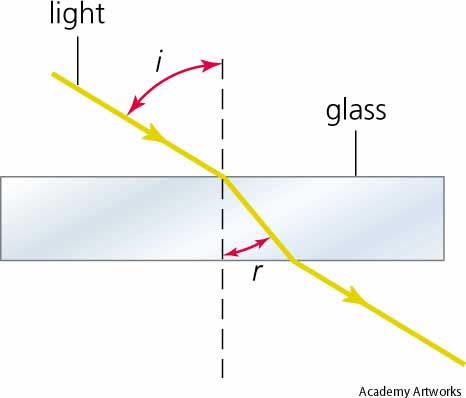
I'm taking my second semester of calc based physics this coming spring. I have a question in optics stemming from my reading of Feynman's lectures on physics. He gives a rough definition of Fermat's principle of least time as follows:
"... out of all possible paths that it might take to get from one point to another, light takes the path which requires the shortest time." (Feynman's emphasis)
My question is this. We know that there exist certain refractive indices for light as it passes through various media. Say we have a rectangular prism. Light is hitting one of the long edges at an angle. According to my understanding of Fermat's PoLT as stated above, the light should travel through the prism forming a right angle at the entry point and a right angle at the exit point (on the inside of the prism). This would minimize the amount of time that the light is in the slow medium, the glass. The total travel time for light would also be minimized, I think.
Of course, this doesn't happen in real life. So my understanding of Fermat's PoLT must be lacking. Could someone explain where I'm going wrong with light and the principle of least time?
Something like this happens in real life: