DocZaius
- 365
- 11
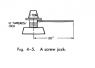
Very early on in Feynman's Lectures on Physics, he offers the example of a screwjack with a mass on it to demonstrate the conservation of energy (picture attached).
He asks how much force would be needed to lift the one ton sitting on top of the screwjack. He then comes up with 1.6 pounds applied to the handle.
Just to make clear I understand, he is saying that when a force of 1.6 pounds is applied to the handle, the system is in equilibrium, right? The mass will technically not lift then, it needs some infinitesimal additional force for the ton to start moving up, right?
He asks how much force would be needed to lift the one ton sitting on top of the screwjack. He then comes up with 1.6 pounds applied to the handle.
Just to make clear I understand, he is saying that when a force of 1.6 pounds is applied to the handle, the system is in equilibrium, right? The mass will technically not lift then, it needs some infinitesimal additional force for the ton to start moving up, right?