Fiber optics: using continous variation refractive indexes hold light?

[tsuwal]

My teacher said that instead of using a fiber optic made of just one material we could use a set of materials with progressively low refractive index to turn the light back in, like so:

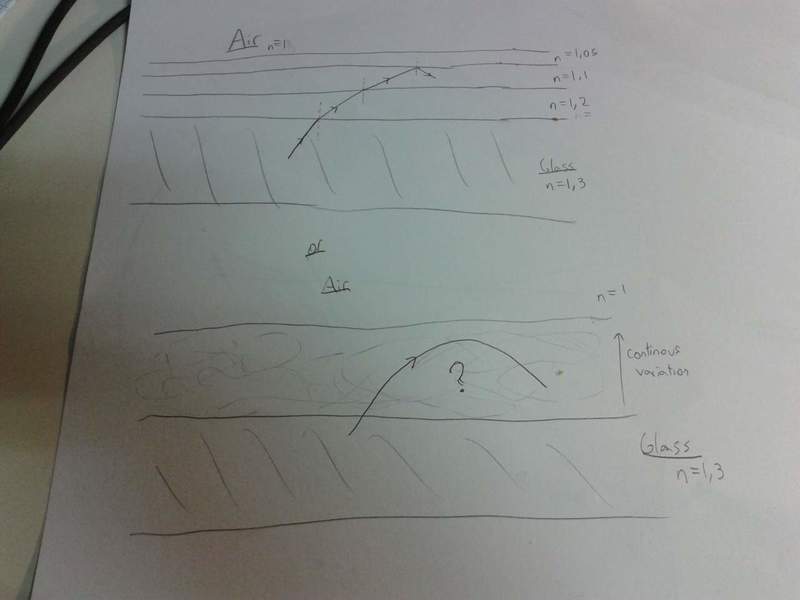
In the case of a continuous variation of refraction index, how can you do the math. Can you please show me, the right way for it?

 

[Drakkith]

Not sure if this will help, but here's the wiki article. It's got some math towards the bottom.
http://en.wikipedia.org/wiki/Gradient-index_optics

 

[tsuwal]

It was a good help, thanks.
The math at the bottom is the fermat principle

$\int_{0}^{end} n ds=minimum$

this is because n=c/velocity, if you take the c out (factorize) you are summing the infinitesimal times of the path the light travels.
However, I can't get anywhere from here, I tried doing the following:

$\int_{0}^{end} n ds=minimum \Leftrightarrow \int_{0}^{maximumheight} n(y)\sqrt{\frac{dx}{dy}^{2}+1} ds=minimum \Rightarrow \frac{d}{dt}\int_{0}^{maximumheight} n(y)\sqrt{\frac{dx}{dy}^{2}+1} ds=0$

we can pass the derivative to the inside of the integral and assume that n(y) varies linearly with y to simplify calculations but anyway, it doesn't like very nice.. Any suggestions?