Figuring Out Clockwise Polygon Fill in a Program

[ZippyDee]

I don't know exactly how to explain this, but I'll try my best:

Let's say I have a set of points (P1, P2, P3...Pn), that are the vertexes of a n-sided polygon. As would be expected, the polygon is drawn simply by connecting the points in order (P1 to P2, P2 to P3, Pn to P1).

This is the hard part to explain...
The lines need to be always drawn "clockwise" rather than "counterclockwise." I'm not sure if that really makes any sense...


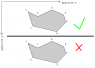
I've attached a picture that may help.

Notice that for the top polygon, when going from any point to the next point (for example P1 to P2), the fill color is always on the right hand side of the line between the points (as if you were standing on P1 and facing P2), but for the bottom polygon, the fill is always to the left of the line.


I know all the x/y coordinates of each point, and therefore can find the angle of any line from one point to another.

How do I mathematically figure out if the filled part is consistently on the right hand side of every line.

Thank you so much in advance!
-Zippy Dee
Ted Newman


Also, please note that this is for a program I am making, so positive Y is moving downward rather than upward.

 

[mikeph]

Can you convert them to polar coordinates and sort them according to their angular coordinate?

Find the angle of point 1, and subtract this angle from every point - an effective coordinate transform to put point 1 on the x-axis. This only works if the shape is convex. Otherwise you could go a longer way- create a vector field modelling the free vortex centered in the middle of the polygon, and perform the line integral around the edge of the polygon. If you go one direction you get a positive circulation, and the other direction you get a negative circulation.

 

[monea83]

Calculate

$$\sum_{i=1}^n x_i y_{i+1} - x_{i+1} y_i$$

in which $$(x_i, y_i)$$ are the coordinates of the vertices. This will give you twice the signed area of the polygon, i.e. if the sign is positive, the ordering is counter-clockwise, otherwise it is clockwise.

 

[ZippyDee]

Awesome, thanks! That's exactly what I was looking for!

 

[ZippyDee]

I just realized that I could also sum up the angles and use that result...I would then either get 360 or -360, unless there were some lines in the polygon that crossed. Which number meant what would depend on whether I sum the interior or exterior angles.