ZippyDee
- 11
- 0
I don't know exactly how to explain this, but I'll try my best:
Let's say I have a set of points (P1, P2, P3...Pn), that are the vertexes of a n-sided polygon. As would be expected, the polygon is drawn simply by connecting the points in order (P1 to P2, P2 to P3, Pn to P1).
This is the hard part to explain...
The lines need to be always drawn "clockwise" rather than "counterclockwise." I'm not sure if that really makes any sense...
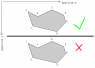
I've attached a picture that may help.
Notice that for the top polygon, when going from any point to the next point (for example P1 to P2), the fill color is always on the right hand side of the line between the points (as if you were standing on P1 and facing P2), but for the bottom polygon, the fill is always to the left of the line.
I know all the x/y coordinates of each point, and therefore can find the angle of any line from one point to another.
How do I mathematically figure out if the filled part is consistently on the right hand side of every line.
Thank you so much in advance!
-Zippy Dee
Ted Newman
Also, please note that this is for a program I am making, so positive Y is moving downward rather than upward.
Let's say I have a set of points (P1, P2, P3...Pn), that are the vertexes of a n-sided polygon. As would be expected, the polygon is drawn simply by connecting the points in order (P1 to P2, P2 to P3, Pn to P1).
This is the hard part to explain...
The lines need to be always drawn "clockwise" rather than "counterclockwise." I'm not sure if that really makes any sense...
I've attached a picture that may help.
Notice that for the top polygon, when going from any point to the next point (for example P1 to P2), the fill color is always on the right hand side of the line between the points (as if you were standing on P1 and facing P2), but for the bottom polygon, the fill is always to the left of the line.
I know all the x/y coordinates of each point, and therefore can find the angle of any line from one point to another.
How do I mathematically figure out if the filled part is consistently on the right hand side of every line.
Thank you so much in advance!
-Zippy Dee
Ted Newman
Also, please note that this is for a program I am making, so positive Y is moving downward rather than upward.