Find a balls speed at a certain time with impulse chart

[Ally385]

Homework Statement

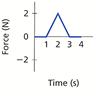
A 0.155-kg ball, moving in the positive direction at 13 m/s, is acted on by the impulse shown in the graph below. What is the ball's speed at 4.0 s?

The graph is attached below.

Homework Equations

J = F Δt

The Attempt at a Solution

I thought that it might be zero because at 4 seconds the force is zero but now I look at it again and I'm thinking the equation might be 0 = 4-0 so the speed would be -4 but that doesn't make since.

 

[HallsofIvy]

Acceleration is proportional to force so acceleration is 0 when force is 0, not velocity. Any velocity increased by the acceleration when force is non-zero is retained when the force returns to 0. "F= ma", of course, so a= F/m and then velocity is the the integral of acceleration. In this problem, rather than finding the equations of those lines and integrating, because the integral can be interpreted as "area under the curve" the velocity is the area of that triangle.

 

[Ally385]

So that would be 2 right? It said that's the wrong answer. Should I not have multiplied the height as 2?

 

[Mandelbroth]

Homework Statement

A 0.155-kg ball, moving in the positive direction at 13 m/s, is acted on by the impulse shown in the graph below. What is the ball's speed at 4.0 s?

$\vec{J} = Δ\vec{p} = \vec{F}Δt$. It looks to me like the impulse is 2 kg m/s.

Thus, $\vec{J} = \vec{p}_{final} - \vec{p}_{initial} = m(\vec{v}_{final} - \vec{v}_{initial})$. Solve for $\vec{v}_{final}$

Hint: Because F = 0 over the interval [3, ∞), the acceleration is 0 in that interval as well. Thus, the velocity is the same at t = 3 as it is at t = 4.