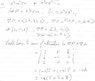Find a vector tangent to the curve of intersection of two cylinders

[s3a]

I have attached both the question and the solution.

I just have questions as to why the solution is the way it is (sorry if they seem stupid but, while I get how to do it mechanically, I don't understand the fundamental reasoning as to why anything is being done):

1) Why are we taking the gradients?
2) Why are we then taking the cross product of the two gradients?

My attempt to answer these questions (I'd still appreciate confirmation for stuff that I am right about):

Gradients at a point in 3D spaces are analogous to derivatives at a point in 2D spaces but taking the gradient of a curve in 3D space yields a normal vector to a point on the curve instead of a line tangent to the curve in the 2D space scenario. I'm guessing these two gradient vectors are supposed to be perpendicular and that finding their cross product would yield a tangent vector to the intersection of the two curves but I don't get why this is so.

Any input would be GREATLY appreciated!
Thanks in advance!

 

[Dick]

Right as far as the gradients being normals to the surfaces. But the two normals don't have to be perpendicular. If n is a normal to surface A at point x, then n is perpendicular to every tangent vector to the surface at x. If your curve is the intersection of the two surfaces then a tangent is a tangent vector to both surfaces. Which means it is perpendicular to both normals. The cross product is a handy way to find a vector that is perpendicular to two given vectors.

 

[s3a]

Thanks a lot!

 

[s3a]

Quick question: The final answer is

T = -4i - 4j + 4k

and not

-4i - 4j - 4k

like the solution says, right? (In other words, there is a "typo", right?)

 

[Dick]

Quick question: The final answer is

T = -4i - 4j + 4k

and not

-4i - 4j - 4k

like the solution says, right? (In other words, there is a "typo", right?)

I seem to be getting -4i - 4j + 4k.

 

[s3a]

Thanks again for the confirmation.