Find distance when slipping down the roof of a sky dome stadium

[totallyclone]

Homework Statement

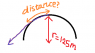
Mike Harris stands at the very top of the sky dome stadium roof to pitch the opening ball for the Blue Jays game. He slips a bit left of centre and slides down along the frictionless roof surface. For what distance, measured along the curve, will he slide before leaving the roof? Assume the roof has a circular cross section of radius 125m.

Homework Equations

F_UN=ma
E_Ti=E_Tf
a=(mv²)/r

The Attempt at a Solution

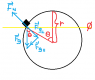
I think, at the point before Mike Harris falls off the roof, F_N=0
So I wonder if this question would involve centripetal forces because the roof is shaped like a circle.

I have attached my diagram and here's how I decided to tackle the question.

F_UN=ma
F_g\bot-F_N=(mv²)/r
mgcosθ-0=[m(2gr(1-cosθ))]/r
cosθ=2(1-cosθ)
cosθ=2-2cosθ
cosθ=2/3
θ=48°

I found the angle, don't quite know how to proceed

 

[mukundpa]

You are correct for the angle and can use

angle (in rad) = arc length / radius

 

[totallyclone]

You are correct for the angle and can use

angle (in rad) = arc length / radius

OOH, so the distance the question is called the arc length? Didn't know that!

So, if I used that formula:

angle (in rad) x radius = arc length
arc length = (48 x ∏/180) x 125
arc length = 105m

So the total distance Mike Harris travels on the sky dome rooftop is 105m?