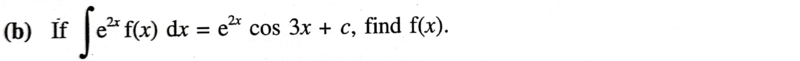Find ##f(x)## in the problem involving integration

Thread starter chwala
Start date Nov 16, 2022
Tags

Integration

In summary, integration is a mathematical process used in scientific research to model and analyze continuous processes. The limits of integration are determined from the given problem and represent the start and end points of the accumulated quantity. There is a difference between definite and indefinite integration, with definite integration giving a specific numerical answer and indefinite integration giving a function that represents a family of possible solutions. Common techniques for solving integration problems include basic integration rules and more advanced techniques, and it is important to double check solutions for accuracy.

Nov 16, 2022

#1

chwala

Gold Member

Homework Statement: see attached

Relevant Equations: integration

Q. 3(b).

This is a textbook problem; unless i am missing something ...the textbook solution is wrong!

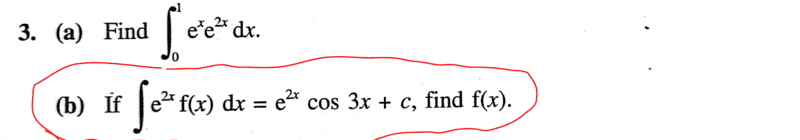
solution;

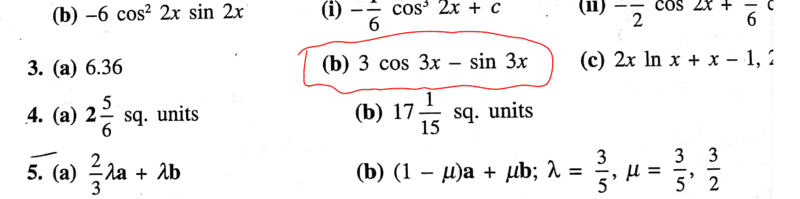
Mythoughts;

##f(x)=2\cos 3x-3\sin 3x## ...by using the product rule on ##\dfrac{d}{dx} (e^{2x} \cos 3x)##.

Physics news on Phys.org

Nov 16, 2022

#2

Staff Emeritus

Science Advisor

Homework Helper

Insights Author

Gold Member

Your solution seems fine.

Nov 17, 2022

#3

Science Advisor

Please get in the habit of posting full problem statements without expressing them exclusively with pictures.

Nov 17, 2022

#4

chwala

Gold Member

nuuskur said:

Please get in the habit of posting full problem statements without expressing them exclusively with pictures.

Noted.

1. What is the purpose of finding ##f(x)## in an integration problem?

The purpose of finding ##f(x)## in an integration problem is to determine the original function from its derivative. Integration is the reverse process of differentiation, and finding ##f(x)## allows us to solve for the function that was differentiated to obtain the given derivative.

2. How do you find ##f(x)## in an integration problem?

To find ##f(x)## in an integration problem, we use the fundamental theorem of calculus. This theorem states that if ##f(x)## is continuous on an interval [a,b] and ##F(x)## is the antiderivative of ##f(x)##, then the definite integral of ##f(x)## from a to b is equal to ##F(b) - F(a)##. Therefore, to find ##f(x)##, we first find the antiderivative of the given function and then evaluate it at the given limits.

3. Can you explain the process of finding ##f(x)## in an integration problem with an example?

Sure, let's say we are given the derivative ##f'(x) = 2x## and we need to find ##f(x)##. We know that the antiderivative of ##2x## is ##x^2 + C##, where C is a constant. So, ##f(x) = x^2 + C##. To find the value of C, we can use the given information that ##f'(x) = 2x##. When we take the derivative of ##x^2 + C##, the constant C disappears, and we are left with ##2x##, which is the given derivative. Therefore, ##f(x) = x^2 + C = x^2##, and we have found ##f(x)##.

4. Are there any shortcuts or tricks to finding ##f(x)## in an integration problem?

Yes, there are some common integration formulas or rules that can be used to find the antiderivative and, therefore, ##f(x)##, more quickly. Some examples include the power rule, the constant multiple rule, and the sum and difference rules. Additionally, there are some integration techniques, such as substitution and integration by parts, that can be used for more complex functions.

5. Is it always possible to find ##f(x)## in an integration problem?

No, it is not always possible to find ##f(x)## in an integration problem. Some functions do not have an elementary antiderivative, meaning they cannot be expressed in terms of basic functions such as polynomials, exponential functions, and trigonometric functions. In these cases, we can still find an approximation of the function using numerical methods, but we cannot find the exact function.

Similar threads

Verify Green's Theorem in the given problem

Mar 9, 2024

Replies: 10

Views: 449

Show that the graph is convex for all values of ##x##

Jun 13, 2023

Replies: 5

Views: 736

Question on Two Differentiation Techniques

Apr 5, 2024

Replies: 25

Views: 354

Find the second derivative of the relation; ##x^2+y^4=10##

Jul 7, 2022

Replies: 24

Views: 2K

Solve the problem involving the given double integral

Dec 6, 2023

Replies: 1

Views: 494

Solving an immediate indefinite integral of a composite function

Mar 8, 2021

Replies: 19

Views: 1K

Minimize integral using orthogonal basis

Jan 24, 2024

Replies: 2

Views: 369

Finding the Fourier Series of a step function

Jan 5, 2021

Replies: 5

Views: 2K

Computing line integral using Stokes' theorem

Dec 11, 2022

Replies: 8

Views: 877

Find the equation of given curve in the form ##e^{3y}=f(x)##

Jun 13, 2022

Replies: 4

Views: 823

Share:

Hot Threads

Recent Insights