LoveBoy
- 44
- 1
Homework Statement
Homework Equations
What is gauge pressure ?
The Attempt at a Solution
How to find gauge pressure ?
Thanks for your explanation .Nathanael said:Gauge pressure is the true pressure minus the ambient air pressure. It can be thought of as "the pressure difference compared to the surface of the liquid." (It is zero at the surface of a liquid. ) Maybe another way to say it is that it is the pressure due only to the weight of the liquid (as opposed to the liquid+atmosphere).
It doesn't make sense to me why they said "Find the force (...) due to gauge pressure" because all of the answers involve the atmospheric pressure... so they are obviously not using the gauge pressure.
I would say just pretend it says "pressure" in place of "gauge pressure."
I don't want to hint at it too much before you attempt the problem, but I will say this much:LoveBoy said:Can you please give me some more hint ?
Cut the sphere into halves, and remove the bottom half. Consider the forces acting on the upper half sphere . The force Fb acting at he base is upward, and there is the downward force Fs on the upper half spherical surface. The result of these forces is the buoyant force, B. You can determine Fb and B, so you get Fs.LoveBoy said:Well , I'm sorry , i can't calculate the answer yet.
Not yet. What is V?LoveBoy said:
Am i right till here ?
By the way,i'm confused in finding the buoyant force i.e weight of fluid displaced .ehild said:B is the buoyant force - it is equal to the weight of the fluid displaced.How much is it?
LoveBoy said:By the way,i'm confused in finding the buoyant force i.e weight of fluid displaced .
LoveBoy said: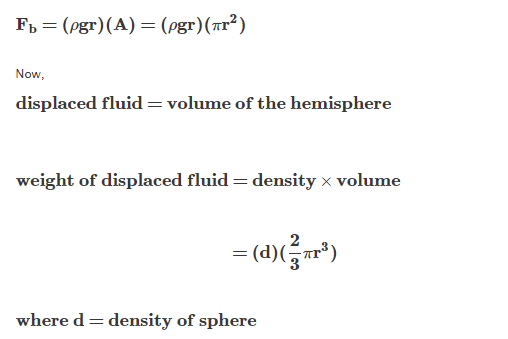
Am i right now ?