Find Hinge Force of Rod Undergoing Circular Motion

[utkarshakash]

Homework Statement

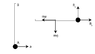
A rod of mass m and length l is hinged about its end A and is vertical initially. Now the end A is accelerated horizontally with acceleration a=g m/s^2. The hinge reaction when the rod becomes horizontal is ?

Homework Equations

See the attached picture for relevant diagrams.

The Attempt at a Solution

When viewed from the frame of the hinge, the rod experiences a pseudo force = ma. Since the rod undergoes circular motion about the hinge A,

$R_x - ma = m \omega ^2 l$

where omega is the angular velocity of the rod when it becomes horizontal. Now I don't know what to write regarding the vertical forces. I'm sure they do not balance each other. Also how do I find omega at the instant?

 

[paisiello2]

Shouldn't l be l/2 in your equation?

I think the vertical forces do balance out so that should be easy.

My suggestion would be to use conservation of energy to get ω.

 

[utkarshakash]

Shouldn't l be l/2 in your equation?

I think the vertical forces do balance out so that should be easy.

My suggestion would be to use conservation of energy to get ω.

Why should it be l/2? If I balance the vertical forces I get R(y) = mg which is wrong according to the answer key.

 

[paisiello2]

The center of mass is located at l/2.

You forgot to include the ma_y of the rod. If you take moments about the hinge then this will cancel with mg leaving R_y = 0.

 

[utkarshakash]

The center of mass is located at l/2.

You forgot to include the ma_y of the rod. If you take moments about the hinge then this will cancel with mg leaving R_y = 0.

But the rod undergoes circular motion about the hinge and not about its COM. R_y is not equal to zero, though.

 

[hav0c]

Can you please clarify whether the rod is in equilibrium in its horizontal position or is it undergoing a circular motion.

 

[utkarshakash]

Can you please clarify whether the rod is in equilibrium in its horizontal position or is it undergoing a circular motion.

The question says that the hinge is being moved. So, I think the rod should undergo circular motion about the hinge. The motion of the rod is a combination of rotational and translational motion when seen from ground. Am I wrong?

 

[Chestermiller]

The question says that the hinge is being moved. So, I think the rod should undergo circular motion about the hinge. The motion of the rod is a combination of rotational and translational motion when seen from ground. Am I wrong?

No. You're correct.

This is not a simple problem, but I can help you work your way through it.

The first thing I always do on a problem like this is to focus on the kinematics of the motion. Let x(t) be the horizontal displacement of the hinge at time t, and let θ(t) be the counterclockwise angle that the rod makes with the vertical y direction. (At time zero, x(0) = 0 and θ(0) = 0.) In terms of x and θ, what are the coordinates x_c and y_c of the center of mass of the rod at time t? What are the x and y components of the velocity of the center of mass of the rod at time t? What are the x and y components of the acceleration of the center of mass of the rod at time t? In terms of θ, what is the angular velocity ω and the angular acceleration α of the rod?

Now you are ready to do force and moment balances on the rod. For an arbitrary value of θ, what are the force balances in the x and y directions? What is the moment balance around the center of mass of the rod?

Incidentally, happy $π$ day everyone.

Chet

 

[paisiello2]

But the rod undergoes circular motion about the hinge and not about its COM. R_y is not equal to zero, though.

Yes, you are right, I'm sorry about that. What I should have said was:

ma_y = mlα/2

where α is the angular acceleration

Take moments about the hinge to solve for α and substitute into the equation for summing forces in the Y direction.

 

[Chestermiller]

Yes, you are right, I'm sorry about that. What I should have said was:

ma_y = mlα/2

where α is the angular acceleration

Take moments about the hinge to solve for α and substitute into the equation for summing forces in the Y direction.

The angular velocity around the center of mass is the same as the angular velocity around the hinge. Just consider the angle that the rod makes with the vertical direction at any point along the rod. It's the same at all locations along the rod.

Chet

 

[paisiello2]

Yes, but taking moments about the hinge eliminates the reaction forces and makes the math simpler I think.

 

[Chestermiller]

Yes, but taking moments about the hinge eliminates the reaction forces and makes the math simpler I think.

OK. Let's see how it plays out. But, don't forget that, for a rigid body, the F = ma equation only applies to the acceleration of the center of mass.

Chet

 

[utkarshakash]

Yes, you are right, I'm sorry about that. What I should have said was:

ma_y = mlα/2

where α is the angular acceleration

Take moments about the hinge to solve for α and substitute into the equation for summing forces in the Y direction.

I could easily get R_y by your method but I'm still having trouble figuring out R_x. Here's what I did:

Initial Potential Energy of the rod = mgl/2 (assuming hinge to be at zero potential)
Let's say the rod acquires a linear velocity v when it becomes horizontal and angular velocity ω.

Final Energy = $\dfrac{ml^2 \omega ^2}{6} + \dfrac{mv^2}{2}$

But the problem is that there is no simple relation between v and ω and thus, I'm left with two variables.

 

[paisiello2]

I think we can set v_y = 0 considering pure rotation.

 

[Chestermiller]

The moment balance on the rod gives:
$$mg\frac{l}{2}sinθ=Iα=\left(\frac{ml^3}{3}\right)\frac{d^2θ}{dt^2}$$
where θ is the angle of the rod measured clockwise from the vertical. Rearranging this gives:
$$\frac{d^2θ}{dt^2}=\frac{3g}{2l}\sinθ$$
If we multiply both sides of this equation by dθ/dt, and integrate with respect to t, we obtain:
$$\left(\frac{dθ}{dt}\right)^2=\frac{3g}{l}(1-\cosθ)$$
When θ=π/2, these equations reduce to:

$$α=\frac{3g}{2l}$$
$$ω^2=\frac{3g}{l}$$

I think these results might help.

Chet

 

[paisiello2]

Not necessary to do all the integration and stuff. Just take moments directly when θ=90° and you get the same answer.

 

[Chestermiller]

Not necessary to do all the integration and stuff. Just take moments directly when θ=90° and you get the same answer.

Really. That's interesting. How did you get the equation for ω² without integrating?

Chet

 

[paisiello2]

I see what you mean. I guess you are solving a differential equation then.

 

[Chestermiller]

I see what you mean. I guess you are solving a differential equation then.

Yes, exactly.

This could also be viewed as a balance between rotational kinetic energy of the rod and gravitational potential energy of the rod, although, to be perfectly frank, it isn't obvious to me how this can be separated in some rational way from the overall mechanical energy balance on the rod. That's an issue that you and the OP were grappling with.

Chet

 

[utkarshakash]

The moment balance on the rod gives:
$$mg\frac{l}{2}sinθ=Iα=\left(\frac{ml^3}{3}\right)\frac{d^2θ}{dt^2}$$
where θ is the angle of the rod measured clockwise from the vertical. Rearranging this gives:
$$\frac{d^2θ}{dt^2}=\frac{3g}{2l}\sinθ$$
If we multiply both sides of this equation by dθ/dt, and integrate with respect to t, we obtain:
$$\left(\frac{dθ}{dt}\right)^2=\frac{3g}{l}(1-\cosθ)$$
When θ=π/2, these equations reduce to:

$$α=\frac{3g}{2l}$$
$$ω^2=\frac{3g}{l}$$

I think these results might help.

Chet

Shouldn't the torque due to pseudo force = ma be included as well?

 

[Chestermiller]

Shouldn't the torque due to pseudo force = ma be included as well?

A pseudo force is not a force. The moment balance is only supposed to include real forces.

Chet

 

[Saitama]

Hi Chestermiller!

I tried the problem following way.

The x-coordinate of CM of rod at any time is:
$$x(t)=\frac{1}{2}gt^2-\frac{l}{2}\sin\theta$$
From Newton's second law:
$$R_x=m\frac{d^2x}{dt^2}$$
Similarly I can write y(t) for CM of rod and then write:
$$mg-R_y=m\frac{d^2y}{dt^2}$$
But I feel what I have done is wrong, how do I introduce the acceleration in my equation given in the problem?

 

[Chestermiller]

Hi Chestermiller!

I tried the problem following way.

The x-coordinate of CM of rod at any time is:
$$x(t)=\frac{1}{2}gt^2-\frac{l}{2}\sin\theta$$
From Newton's second law:
$$R_x=m\frac{d^2x}{dt^2}$$
Similarly I can write y(t) for CM of rod and then write:
$$mg-R_y=m\frac{d^2y}{dt^2}$$
But I feel what I have done is wrong, how do I introduce the acceleration in my equation given in the problem?

The x and y coordinates of the center of mass is given by:
$$x_c(t)=x(t)-\frac{l}{2}\sinθ$$
$$y_c(t)=\frac{l}{2}\cosθ$$
where x(t) is the x coordinate of the hinge at time t.
From this, the velocity components of the center of mass are given by:
$$v_{cx}(t)=v(t)-\frac{l}{2}\cosθ\frac{dθ}{dt}$$
$$v_{cy}(t)=-\frac{l}{2}\sinθ\frac{dθ}{dt}$$
From this, the acceleration components of the center of mass are given by:
$$a_{cx}(t)=a-\frac{l}{2}\cosθ\frac{d^2θ}{dt^2}+ \frac{l}{2}\sinθ\left(\frac{dθ}{dt}\right)^2$$
$$a_{cy}(t)=-\frac{l}{2}\sinθ\frac{d^2θ}{dt^2}-\frac{l}{2}\cosθ\left(\frac{dθ}{dt}\right)^2$$
where a is the acceleration of the hinge.
So, the force balances in the x and y directions can be written:
$$ma_{cx}=R_x$$
$$ma_{cy}=R_y-mg$$
Chet

 

[Saitama]

The x and y coordinates of the center of mass is given by:
$$x_c(t)=x(t)-\frac{l}{2}\sinθ$$
$$y_c(t)=\frac{l}{2}\cosθ$$
where x(t) is the x coordinate of the hinge at time t.

I am sorry if I am missing something but isn't that what I have written?

A few posts ago, you found $\omega^2$ as a function of $\theta$, I am wondering if it was necessary, can't we directly use energy conservation to find $\omega^2$ at $\theta=\pi/2$?

 

[Chestermiller]

I am sorry if I am missing something but isn't that what I have written?

A few posts ago, you found $\omega^2$ as a function of $\theta$, I am wondering if it was necessary, can't we directly use energy conservation to find $\omega^2$ at $\theta=\pi/2$?

I guess, yes, except for the g in the equation for x, rather than an a.

If you can find $\omega^2$ at $\theta=\pi/2$ with overall energy conservation, that would be great. Please show how? The only way I was able to do it was with the moment balance. Probably, I'm missing something.

Chet

 

[Saitama]

I guess, yes, except for the g in the equation for x, rather than an a.

The problem statement mentions that $a=g$. :)

If you can find $\omega^2$ at $\theta=\pi/2$ with overall energy conservation, that would be great. Please show how? The only way I was able to do it was with the moment balance. Probably, I'm missing something.

Chet

I did say "I am wondering". :P

I think you are right but please look at the following, something doesn't look right. :(

From energy conservation,
$$mg\frac{l}{2}=\frac{1}{2}\frac{ml^2}{3}\omega^2+\frac{1}{2}mv^2$$
$$\Rightarrow gl=\frac{l^2\omega^2}{3}+v^2$$
From the equations you wrote:
$$v^2=v^2_{cx}(t)+v^2_{cy}(t)=g^2t^2+\frac{l^2}{4}\omega^2-gtl\cos\theta \omega$$
At $\theta=\pi/2$, the above becomes:
$$v^2=g^2t^2+\frac{l^2}{4}\frac{3g}{l}=g^2t^2+\frac{3gl}{4}$$
Substituting in the energy equation and solving for $t^2$ gives a negative answer. :(

 

[Tanya Sharma]

Energy conservation can not be applied in this problem.

 

[Saitama]

Energy is definitely not conserved .

Erm...why not?

 

[Tanya Sharma]

Are you completely sure there is no work done by any force on the rod ?

 

[Saitama]

Are you completely sure there is no work done being done by any force on the rod ?

The external force which is accelerating the rod also does work on the rod, right?

 

[Tanya Sharma]

Correct...So forget energy conservation :)

 

[Saitama]

Correct...So forget energy conservation :)

Thanks! :)

 

[Tanya Sharma]

We need another equation apart from the last four equations by Chet in post#23

 

[Saitama]

We need another equation apart from the last four equations by Chet in post#23

Are you talking about this?

https://www.physicsforums.com/showpost.php?p=4689443&postcount=15

I think we don't need the equations from #23, page 1 of this thread has it all. Chestermiller derived $\omega^2$ and $\alpha$ as a function of $\theta$ in post #15 and I suppose that is sufficient. Next step is to apply Newton's second law.

 

[Tanya Sharma]

Are you talking about this?

https://www.physicsforums.com/showpost.php?p=4689443&postcount=15

I think we don't need the equations from #23, page 1 of this thread has it all. Chestermiller derived $\omega^2$ and $\alpha$ as a function of $\theta$ in post #15 and I suppose that is sufficient. Next step is to apply Newton's second law.

I may be wrong but I think the equation in post#15 is incorrect .You cannot write torque equation about the hinge .

In this problem it has to be written about the COM.