Here is another method, maybe a bit more simple, where practical issues like inclusion of the border or numerical stability are perhaps easier to control.
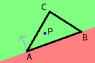
The following procedure is repeated 3 times, once for each side of the triangle. In the attached picture, representing one of the three iterations using side AB, the idea is to determine if the given point is in the "green area", on the same side of the line as the triangle itself. (If this is true for the three sides, then the point is inside.) I use a vector perpendicular to the line, as drawn in the picture. If the vector from vertex A to vertex B is (p,q) = (Bx-Ax, By-Ay), then a perpendicular vector could be (-q,p). Now, a dot product between this perpendicular vector and any other vector (in particular, the vector from A to our given point P) will be positive on one side of the line, and negative on the other; we can use this sign to discern at which side any point lies. But there is a caveat: we don't really know towards which side (green or red) the perpendicular vector will point to (due to the simplistic way in which it was calculated; forcing it to the actual green side would require a good number of extra tests). In the picture it is on the green side, but it could have been just as perpendicular but on the red side. What I do is to use, as a reference, the sign of the dot product between the perpendicular vector and the vector from A to C (since C is always on the green side, on the side that contains the triangle).
The dot product of two vectors, Ux,Uy and Vx,Vy, is of course UxVx + UyVy.