Find induced charge on conducting cube in uniform field

[Samuelriesterer]

Problem statement, equations, and work done:

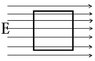
A perfectly conducting cube is placed in a uniform electric field in the x direction (see attached).

Step1 : Use Gauss's law to determine the electric field inside the cube.$\phi_E = 2E(r)A = \frac{q}{\epsilon_0} → E(r)=\frac{\sigma}{2\epsilon_0}$Step2: The field inside the cube is the superposition of the uniform field and the field due to any charge induced on the cube. In the approximation that the cube is very large, what is the induced charge density near the centers of the left and right faces of the cube (in terms of the external field E).

This is where I am stuck. I don't quite understand this. Wouldn't this be:

$q=\sigma A = 2AE(r)\epsilon_0$

Step3: Sketch the field inside the cube due to the induced charge, assuming the charge density on the faces is the same as the density at the center of the face.Step4 : NONCALCULATIONAL In order to exactly cancel the uniform field inside the cube, what would need to change about the charge distribution?How does your answer work with the behavior of charges on a perfect conductor?

 

[Orodruin]

Step1 : Use Gauss's law to determine the electric field inside the cube.$\phi_E = 2E(r)A = \frac{q}{\epsilon_0} → E(r)=\frac{\sigma}{2\epsilon_0}$

You do not yet know what $\sigma$ is so you really cannot use it to answer this question. You can solve for the electric field inside the cube without knowing anything about the charge density and/or the external field simply from the knowledge that the cube is conducting and therefore equipotential.

 

[Samuelriesterer]

So the field inside the cube would be:

$ϕ_E=2E(r)A=q/\epsilon_0 = 0$

But what about the induced charge density? What is inducing it?

 

[Orodruin]

Now consider the full space as your system. You know the field everywhere. How do you relate the field to the charge density?

What is inducing it?

The external field is. In order to maintain equipotential on the cube, there needs to be a charge arrangement such that the cube does not only have the external field.

 

[Samuelriesterer]

Now consider the full space as your system. You know the field everywhere. How do you relate the field to the charge density?.

Would this be:

$\sigma = E \epsilon_0$

 

[Samuelriesterer]

I'm not sure how to draw a field inside the cube if the net field inside is zero?

 

[Orodruin]

The point is the following: The outside field cannot be constant. The addition of the equipotential cube will lead to an additional field outside of the box as well (just as it cancels the field inside the box.

In order to find the charge density, you would take the divergence of the electric field according to Gauss' law, but you would first need the field outside of the box as well.

Your problem statement tells you to find the charge density in the centre if the cube is large. In that case the electric field just outside will be the old external field $\vec E$. In step 3 you are asked to draw the field if the charge density on the entire face was that computed in step 2. The field will be non-zero, because this is not the field configuration for a perfect conductor. For a perfect conductor the charge distribution will not be uniform across the top and bottom faces. This is what you are asked to discuss in step 4.

 

[Samuelriesterer]

So in order to cancel the uniform field exactly you would need the charge distribution to be even throughout the whole cube even the top and bottom.

Is the cube simply polarized because of the external field? Or is it conducting a charge?

I am envisioning something like the right image if the attached picture. I just don't get this stuff despite studying the last 4 hours.

 

[Orodruin]

So in order to cancel the uniform field exactly you would need the charge distribution to be even throughout the whole cube even the top and bottom.

No, this is the entire point. You are being asked how it will look with an even charge distribution on the top and bottom. This will not cancel the field inside the cube. In order to do this you will need a charge distribution which is not even throughout.

Is the cube simply polarized because of the external field?

The cube is a conductor, which will make it equipotential. It would not be polarised without the external field, nor without being a conductor.

 

[Orodruin]

So in order to cancel the uniform field exactly you would need the charge distribution to be even throughout the whole cube even the top and bottom.

No, this is the entire point. You are being asked how it will look with an even charge distribution on the top and bottom. This will not cancel the field inside the cube. In order to do this you will need a charge distribution which is not even throughout.

Is the cube simply polarized because of the external field?

The cube is a conductor, which will make it equipotential. It would not be polarised without the external field, nor without being a conductor.