MHB Find Length of Line D in ABC Triangle

[MarkFL]

Here is the question:

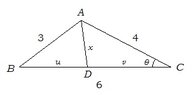
How will you find the length of a line drawn inside a scalene triangle?


ABC is a scalene triangle, in which AB = 3, AC = 4 and BC = 6
D is the line joining A with BC.such that BD : DC : :2 :3

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Re: Sepia's question ay Yahoo! Answers regarding finding the length of a line segment within a trian

Hello Sepia,

Let's first draw a diagram:

View attachment 1408

We see that:

$$u+v=6$$

and we are given:

$$\frac{u}{v}=\frac{2}{3}\implies u=\frac{2}{3}v$$

Substituting this into the first equation, we then find:

$$\frac{2}{3}v+v=6$$

$$\frac{5}{3}v=6$$

$$v=\frac{18}{5}$$

Now, let's use the Law of Cosines to determine the cosine of the angle $\theta$:

$$3^2=4^2+6^2-2\cdot4\cdot6\cos(\theta)$$

$$\cos(\theta)=\frac{4^2+6^2-3^2}{2\cdot4\cdot6}=\frac{43}{48}$$

Next, using the Law of Cosines again, we may state:

$$x=\sqrt{4^2+v^2-2\cdot4\cdot v\cos(\theta)}$$

$$x=\sqrt{4^2+\left(\frac{18}{5} \right)^2-2\cdot4\cdot\left(\frac{18}{5} \right)\left(\frac{43}{48} \right)}=\frac{\sqrt{79}}{5}$$