Find Next Smallest & Greatest Key in BST

[evinda]

Hello! (Wave)

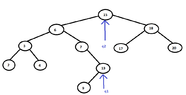
We consider a Binary search tree and we want to find the element with the next greatest and the next smallest key than the key of a node v.

For example, how can we find the next of the node to which q1 points in the in-order traversal?

How will we find the next of the node to which q2 points, in the in-order traversal?

View attachment 3877Will it be as follows?

If we have a pointer to the root, the element with the next smallest key will be the rightmost child of the left subtree of the root and the element with the next greatest key will be the leftmost child of the right subtree of the root.

If we have a pointer to a node v of which the key is smaller than this of the root, then the rightmost child of the left subtree of v will have the key with the next smallest element and the first right child will have the next greatest key.

If we have a pointer to a node v of which the key is greater than this of the root, then the rightmost child of the left subtree of v will have the key with the next smallest element and the leftmost child of the right subtree will have the next greatest key.

Or have I understood it wrong? (Thinking)

 

[lofgran]

Hello!

Your understanding of finding the next greatest and smallest keys in a binary search tree is generally correct. However, there are a few clarifications that can be made.

First, it is important to note that in-order traversal in a binary search tree follows the pattern of left subtree, current node, right subtree. So, in order to find the next greatest and smallest keys, we need to consider the nodes in the order of left, current, and then right.

In the case of q1, if the node to which it points has a right child, then the next greatest key will be the leftmost child of that right subtree. If the node does not have a right child, then we need to backtrack to its parent and check if it is a left child. If it is, then the parent node will have the next greatest key. If it is a right child, we need to backtrack further until we find a node that is a left child, and that node will have the next greatest key.

For q2, we need to follow a similar approach. If the node to which it points has a left child, then the next smallest key will be the rightmost child of that left subtree. If the node does not have a left child, then we need to backtrack to its parent and check if it is a right child. If it is, then the parent node will have the next smallest key. If it is a left child, we need to backtrack further until we find a node that is a right child, and that node will have the next smallest key.

I hope this helps clarify any confusion. Let me know if you have any further questions.