aaaa202
- 1,144
- 2
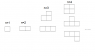
In the picture attached I have tried to list the different shapes you can get when you attach, 1, 2, 3, 4 squares, but, as you can imagine, when n gets bigger the number of combinations gets incredibly large. Is there are way to see how many possible configurations there is for n squares, and the different perimeters of these shapes?
If not is it possible for equilateral triangles?
If not is it possible for equilateral triangles?
Attachments
Last edited: